题目内容

18．已知关于x的不等式mx2-x+m＜0的解是一切实数，求m的取值范围．

分析 当m=0时，不等式可化为-x＜0，显然x不是一切实数，当m≠0时，不等式mx2-x+m＜0的解是一切实数，则对应的二次函数y=mx2-x+m的图象应开口朝下，且与x轴没有交点，由此构造不等式组，最后综合讨论结果，可得答案．

解答 解：当m=0时，不等式可化为-x＜0，显然x不是一切实数，
当m≠0时，不等式mx2-x+m＜0的解是一切实数
则对应的二次函数y=mx2-x+m的图象应开口朝下，且与x轴没有交点，
故$\left\{\begin{array}{l}{m＜0}\\{1-4{m}^{2}＜0}\end{array}\right.$，解得m＜-$\frac{1}{2}$，
综上所述，实数m的取值范围是m＜-$\frac{1}{2}$．

点评 本题考查的知识点是一元二次不等式的应用，其中解答时易忽略m=0时，不等式可化为4＞0，满足条件而错解为0＜m＜4．

练习册系列答案
相关题目
17．已知非零向量$\overrightarrow{a}$与$\overrightarrow{b}$，$\overrightarrow{c}$=$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{d}$=$\overrightarrow{a}$-$\overrightarrow{b}$，如果$\overrightarrow{c}$∥$\overrightarrow{d}$，求证：$\overrightarrow{a}$∥$\overrightarrow{b}$．
18．若f（$\sqrt{x}+2$）=x+6$\sqrt{x}$+3，则f（x）=x2+2x-5，（x≥2）．
6．已知圆M过点C（1，-1），D（-1，1），且圆心M在x+y-2=0上．
（1）求圆M的方程；
（2）设P（x，y）是圆M上任意一点求x+y的取值范围．
13．（x2+1）（$\frac{1}{{x}^{2}}$-mx）5展开式中x2项的系数125，求m的值．
3．若$\root{2n}{x+1}$+（x-1）0（n∈N，n＞1）有意义，则x的取值范围是{x|x≥-1，x≠1}．
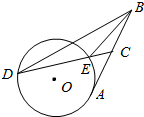10．如图，AB为圆O的切线，A为切点，过线段AB上一点C作圆O的割线CED（E在C、D之间），且∠BEC=∠DBC，求证：BC=CA．
7．若θ∈（0，π），cosθ=-$\frac{1}{3}$，则tanθ=-2$\sqrt{2}$．
8．若3sinθ=cosθ，则cos2θ+sin 2θ的值等于$\frac{7}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网