题目内容
13.(x2+1)($\frac{1}{{x}^{2}}$-mx)5展开式中x2项的系数125,求m的值.分析 把($\frac{1}{{x}^{2}}$-mx)5 按照二项式定理展开,可得(x2+1)($\frac{1}{{x}^{2}}$-mx)5展开式中x2项的系数,再根据x2项的系数为125,求得m的值.
解答 解:∵(x2+1)($\frac{1}{{x}^{2}}$-mx)5 =(x2+1)(${C}_{5}^{0}$•x-10-m${C}_{5}^{1}$•x-7+m2${C}_{5}^{2}$•x-4-m3 ${C}_{5}^{3}$•x-1+m4 ${C}_{5}^{4}$•x2-m5${C}_{5}^{5}$•x5 ),
∴展开式中x2项的系数为m4•${C}_{5}^{4}$=125,∴m±$\sqrt{5}$.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
相关题目
12.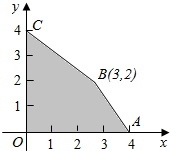 如图所示,目标函数z=kx-y的可行域为四边形OABC,点B(3,2)是目标函数最优解,则k的取值范围( )
如图所示,目标函数z=kx-y的可行域为四边形OABC,点B(3,2)是目标函数最优解,则k的取值范围( )
 如图所示,目标函数z=kx-y的可行域为四边形OABC,点B(3,2)是目标函数最优解,则k的取值范围( )
如图所示,目标函数z=kx-y的可行域为四边形OABC,点B(3,2)是目标函数最优解,则k的取值范围( )| A. | ($\frac{2}{3}$,2) | B. | (1,$\frac{5}{3}$) | C. | (-2,-$\frac{2}{3}$) | D. | (-3,-$\frac{4}{3}$) |
1. 如图所示,正三角形ABC的边长为2,其外接圆为圆O,点D为劣弧AB上一个动点(不与点重合),过点D与AB的中心P的直线交圆O于另一点E,则$\frac{2}{3}$EP+DP的最小值为( )
如图所示,正三角形ABC的边长为2,其外接圆为圆O,点D为劣弧AB上一个动点(不与点重合),过点D与AB的中心P的直线交圆O于另一点E,则$\frac{2}{3}$EP+DP的最小值为( )
 如图所示,正三角形ABC的边长为2,其外接圆为圆O,点D为劣弧AB上一个动点(不与点重合),过点D与AB的中心P的直线交圆O于另一点E,则$\frac{2}{3}$EP+DP的最小值为( )
如图所示,正三角形ABC的边长为2,其外接圆为圆O,点D为劣弧AB上一个动点(不与点重合),过点D与AB的中心P的直线交圆O于另一点E,则$\frac{2}{3}$EP+DP的最小值为( )| A. | $\sqrt{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2}{3}$$\sqrt{6}$ |
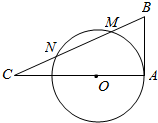 如图所示,已知AD为⊙O的直径,AB为⊙O的切线,割线BN的延长线交AD的延长线于点C,且BM=MN=NC,若AB=2,则该圆的直径AD的长为$\frac{5}{7}\sqrt{14}$.
如图所示,已知AD为⊙O的直径,AB为⊙O的切线,割线BN的延长线交AD的延长线于点C,且BM=MN=NC,若AB=2,则该圆的直径AD的长为$\frac{5}{7}\sqrt{14}$.