Question

10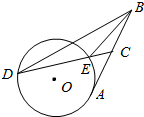．如图，AB为圆O的切线，A为切点，过线段AB上一点C作圆O的割线CED（E在C、D之间），且∠BEC=∠DBC，求证：BC=CA．

Answer 1

分析 由已知条件推导出△BCE∽△DCB，从而BC²=EC•DC，由切割线定理得CA²=CE•CD，由此能证明BC=CA．

解答 证明：在△BCE和△DCB中，
∵∠BCE=∠DCB，∠CBE=∠CDB，
∴△BCE∽△DCB，
∴$\frac{BC}{DC}$=$\frac{EC}{BC}$，
∴BC²=EC•DC，
∵直线AB，直线CDE分别是⊙O的切线和割线，
∴由切割线定理得CA²=CE•CD，
∴BC²=CA²，
∴BC=CA．

点评 本题考查点是线段中点的证明，是中档题，解题时要注意三角形相似和切割线定理的合理运用．