题目内容
7．
如图，在四边形ABCD中，AB⊥BC，AB=3，BC=4，△ACD是等边三角形，则$\overrightarrow{AC}•\overrightarrow{BD}$的值为$\frac{7}{2}$．
分析 通过题意可知AD=AC=5，cos∠CAD=$\frac{1}{2}$，cos∠BAC=$\frac{3}{5}$，利用$\overrightarrow{AC}•\overrightarrow{BD}$=$\overrightarrow{AC}$•$\overrightarrow{AD}$-$\overrightarrow{AC}$•$\overrightarrow{AB}$，代入计算即可．
解答 解：∵AB⊥BC，AB=3，BC=4，
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5，cos∠BAC=$\frac{3}{5}$，
又∵△ACD是等边三角形，
∴AD=AC=5，cos∠CAD=$\frac{1}{2}$，
∴$\overrightarrow{AC}•\overrightarrow{BD}$
=$\overrightarrow{AC}$•（$\overrightarrow{AD}$-$\overrightarrow{AB}$）
=$\overrightarrow{AC}$•$\overrightarrow{AD}$-$\overrightarrow{AC}$•$\overrightarrow{AB}$
=$5×5×\frac{1}{2}$-$5×3×\frac{3}{5}$
=$\frac{7}{2}$，
故答案为：$\frac{7}{2}$．
点评 本题考查平面向量数量积的运算，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
18．某家电产品受在保修期内维修费等因素的影响，企业生产每件的利润与该产品首次出现故障的时间有关．某厂家生产甲、乙两种品牌，保修期均为2年．现从该厂已售出的两种品牌家电中各随机抽取50件，统计数据如下：
将频率视为概率，解答下列问题：
（Ⅰ）从该厂生产的甲、乙品牌产品中随机各抽取一件，求其至少有一件首次出现故障发生在保修期内的概率；
（Ⅱ）若该厂生产的家电均能售出，记生产一件甲品牌的利润为X1，生产一件乙品牌家电的利润为X2，分别求X1，X2的分布列；
（Ⅲ）该厂预计今后这两种品牌家电销量相当，由于资金限制，只能生产其中一种品牌的家电．若从经济效益的角度考虑，你认为应生产哪种品牌的家电？说明理由．
| 品牌 | 甲 | 乙 | |||
| 首次出现故障时间x（年） | 0＜x≤1 | 1＜x≤2 | x＞2 | 0＜x≤2 | x＞2 |
| 数量（件） | 2 | 3 | 45 | 5 | 45 |
| 每件利润（百元） | 1 | 2 | 3 | 1.8 | 2.9 |
（Ⅰ）从该厂生产的甲、乙品牌产品中随机各抽取一件，求其至少有一件首次出现故障发生在保修期内的概率；
（Ⅱ）若该厂生产的家电均能售出，记生产一件甲品牌的利润为X1，生产一件乙品牌家电的利润为X2，分别求X1，X2的分布列；
（Ⅲ）该厂预计今后这两种品牌家电销量相当，由于资金限制，只能生产其中一种品牌的家电．若从经济效益的角度考虑，你认为应生产哪种品牌的家电？说明理由．
15．已知直线m，l，平面α，β，且m⊥α，l?β，给出下列命题：①若α∥β，则m⊥l； ②若α⊥β，则m∥l； ③若m⊥l，则α⊥β； ④若m∥l，则α⊥β．其中正确的命题的是（ ）
| A． | ①② | B． | ③④ | C． | ①④ | D． | ①③ |
2．在△ABC中，角A、B、C的对边分别为a，b，c，且满足$\sqrt{2}$acosB=bcosC+ccosB，则角B的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
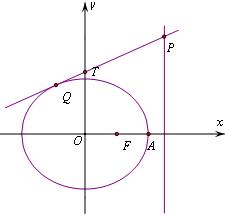如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，右焦点为F，右顶点为A，P为直线x=$\frac{5}{4}$a上的任意一点，且（$\overrightarrow{PF}$+$\overrightarrow{PA}$）•$\overrightarrow{AF}$=2．