题目内容
【题目】已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的2倍且经过点M（2，1），平行于OM的直线l在y轴上的截距为m（m≠0），l交椭圆于A、B两个不同点．
（1）求椭圆的标准方程以及m的取值范围；
（2）求证直线MA，MB与x轴始终围成一个等腰三角形．
【答案】
（1）解：设椭圆方程为 
（a＞b＞0），且a=2b，
椭圆经过点M（2，1），则 
，解得：a=2 
，b= ，
∴椭圆方程 
；
∵直线l平行于OM，且在y轴上的截距为m 又kOM= 
，
∴l的方程为：y= x+m，
由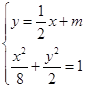 
，整理得：x2+2mx+2m2﹣4=0
∵直线l与椭圆交于A、B两个不同点，△=（2m）2﹣4（2m2﹣4）＞0，解得：﹣2＜m＜0或0＜m＜2，
∴m的取值范围是（﹣2，0）∪（0，2）
（2）证明：设直线MA、MB的斜率分别为k1，k2，
要证直线MA，MB与x轴始终围成一个等腰三角形．只需证明k1+k2=0．
设A（x1，y1），B（x2，y2），l的方程为：y= x+m，则k1= 
，k2= 
．
由 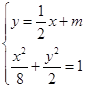，整理得：x2+2mx+2m2﹣4=0
∴x1+x2=﹣2m，x1x2=2m2﹣4，
而k1+k2= + = 
，
其分子=（ x1+m﹣1）（x2﹣2）+（ x2+m﹣1）（x1﹣2）
=x1x2+（m﹣2）（x1+x2）﹣4（m﹣1）=2m2﹣4﹣2m（m﹣2）﹣4m+4=0，
∴k1+k2=0．
故直线MA、MB与x轴始终围成一个等腰三角形
【解析】（1）根据题意，将M点代入即可求得a和b的值，即可求得椭圆方程，求得直线l的方程，代入椭圆方程，由△＞0即可求得m的取值范围；（2）设直线MA、MB的斜率分别为k1，k2，只需证明k1+k2=0即可，根据直线的斜率公式及韦达定理即可求得答案．
【题目】某校为评估新教改对教学的影响，挑选了水平相当的两个平行班进行对比实验．甲班采用创新教法，乙班仍采用传统教法，一段时间后进行水平测试，成绩结果全部落在[60，100]区间内（满分100分），并绘制频率分布直方图如图，两个班人数均为60人，成绩80分及以上为优良． 
（1）根据以上信息填好2×2联表，并判断出有多大的把握认为学生
（2）成绩优良与班级有关？
（3）以班级分层抽样，抽取成绩优良的5人参加座谈，现从5人中随机选3人来作书面发言，求发言人至少有2人来自甲班的概率．（以下临界值及公式仅供参考）
P（k2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
k2= 
，n=a+b+c+d．
