题目内容
18. 已知函数g(x)=Acos(?x+ϕ)(A>0,?>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示,f(x)的图象可由g(x)的图象向左平移2个单位得到,则f(1)+f(2)+…+f(2004)=( )
已知函数g(x)=Acos(?x+ϕ)(A>0,?>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示,f(x)的图象可由g(x)的图象向左平移2个单位得到,则f(1)+f(2)+…+f(2004)=( )| A. | 1 | B. | 3$+\sqrt{3}$ | C. | 2+$\sqrt{3}$ | D. | 0 |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,再利用函数的周期性求得所给式子的值.
解答 解:根据函数g(x)=Acos(?x+ϕ)(A>0,?>0,|ϕ|<$\frac{π}{2}$)的部分图象,可得A=2,
$\frac{T}{2}$=$\frac{1}{2}$•$\frac{2π}{ω}$=8-2,∴ω=$\frac{π}{6}$.
又g(x)在x=2处取得最大值,有2×$\frac{π}{6}$+ϕ=2kπ,|ϕ|<$\frac{π}{2}$,所以取ϕ=-$\frac{π}{3}$;
g(x)=2cos($\frac{π}{6}$x-$\frac{π}{3}$);
f(x)的图象可由g(x)的图象向左平移2个单位得到,所以f(x)=2cos($\frac{π}{6}$x);
由于周期为12,则f(1)+f(2)+…+f(12)=0,
故则f(1)+f(2)+…+f(2004)=167×[f(1)+f(2)+…+f(12)]=0,
故选:D.
点评 作为选择题,求出f(x)和g(x)周期为12,意识到2014恰好为12的倍数,可以直接得出答案,效率大大提高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.对于函数y=f(x),当x∈(0,+∞)时,总有f(x)<xf′(x),若m>n>0,则下列不等式中,恒成立的是( )
| A. | $\frac{f(m)}{n}$<$\frac{f(n)}{m}$ | B. | $\frac{f(m)}{m}$<$\frac{f(n)}{n}$ | C. | $\frac{f(m)}{n}$>$\frac{3f(n)}{m}$ | D. | $\frac{f(m)}{m}$>$\frac{f(n)}{n}$ |
9.设定义在R上的奇函数f(x)在区间(0,+∞)上单调递增,则不等式f(x-1)<0的解集是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (-∞,0) |
6.如图⊙O中,弦AB与弦CD相交于点P,∠B=38°,∠APD=80°,则∠A等于( )
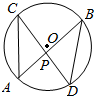

| A. | 38° | B. | 42° | C. | 80° | D. | 118° |
3.设(x+3)(2x+3)10=a0+a1(x+3)+a2(x+3)2+…+a11(x+3)11,则a0+a1+a2+…+a11的值为( )
| A. | 1 | B. | 2 | C. | 311 | D. | 4×510 |
8.iPhone 6是苹果公司(Apple)在2014年9月9日推出的一款手机,已于9月19日正式上市.据统计发现该产品的广告费用x与销售额y的统计数据如表:
根据上表可得回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\stackrel{∧}{b}$为9.4,据此模型预报广告费用为6百万元时销售额为( )
| 广告费用x(百万元) | 4 | 2 | 3 | 5 |
| 销售额y(百万元) | 44 | 25 | 37 | 54 |
| A. | 61.5百万元 | B. | 62.5百万元 | C. | 63.5百万元 | D. | 65.0百万元 |