题目内容
【题目】某城市先后采用甲、乙两种方案治理空气污染各一年,各自随机抽取一年(365天)内100天的空气质量指数API的检测数据进行分析,若空气质量指数值在[0,300]内为合格,否则为不合格.表1是甲方案检测数据样本的频数分布表,如图是乙方案检测数据样本的频率分布直方图.
表1:
API值 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | 大于300 |
天数 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
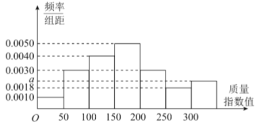
(1)将频率视为概率,求乙方案样本的频率分布直方图中![]() 的值,以及乙方案样本的空气质量不合格天数;
的值,以及乙方案样本的空气质量不合格天数;
(2)求乙方案样木的中位数;
(3)填写下面2×2列联表(如表2),并根据列联表判断是否有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.
表2:
甲方案 | 乙方案 | 合计 | |
合格天数 | _______ | _______ | _______ |
不合格天数 | _______ | _______ | _______ |
合计 | _______ | _______ | _______ |
附: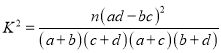
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
【答案】(1)![]() ,11天;(2)170;(3)表格见解析,有90%的把握认为该城市的空气质量指数值与两种方案的选择有关
,11天;(2)170;(3)表格见解析,有90%的把握认为该城市的空气质量指数值与两种方案的选择有关
【解析】
(1)根据频率和为1列出等式求解a,用乙方案样本中空气质量指数值大于300的频率乘以总天数即可得解;(2)根据中位数左边和右边的小长方形的面积和是相等的列出等式即可求得中位数;(3)由题意填写列联表,计算观测值,对照临界值得出结论.
(1)由频率分布直方图知,
![]() ,
,
解得![]() ,
,
∴乙方案样本中不合格天数为![]() (天);
(天);
(2)根据图1,得![]() ,
,
又![]() ,∵
,∵![]() ,
,
∴中位数在(150,200]之间,设中位数为![]() ,
,
则![]() ,解得
,解得![]() ,
,
∴乙方案样本的中位数为170;
(3)由题意填写![]() 列联表如下,
列联表如下,
甲方案 | 乙方案 | 合计 | |
合格天数 | 96 | 89 | 185 |
不合格天数 | 4 | 11 | 15 |
合计 | 100 | 100 | 200 |
由表中数据,计算![]() ,
,
![]()
![]() ,
,
∴有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.