题目内容
【题目】已知函数![]()
(1)若f(x)在[0,2]上是单调函数,求a的值;
(2)已知对![]() ∈[1,2],f(x)≤1均成立,求a的取值范围.
∈[1,2],f(x)≤1均成立,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据![]() 求导,令
求导,令![]() 解得
解得![]() ,
,![]() ,然后分
,然后分![]()
![]()
![]() 讨论求解.
讨论求解.
(2)解法一:根据“对![]() ,
,![]() 均成立”,则
均成立”,则![]() 成立,得到
成立,得到![]() ,则
,则![]() 结合(1),
结合(1),![]() 时,
时,![]() ,
,![]() 在
在![]() 上增,将“对
上增,将“对![]() ,
,![]() 均成立”转化为
均成立”转化为![]() 求解即可.
求解即可.
(1)因为![]()
所以![]() ,
,
令![]() 解得
解得![]() ,
,![]() .
.
若![]() 即
即![]() ,
,
则![]() 对
对![]() 成立,函数
成立,函数![]() 在
在![]() 上单调,符合题目要求;
上单调,符合题目要求;
若![]() 即
即![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
函数![]() 在
在![]() 上不单调,不符合题目要求;
上不单调,不符合题目要求;
若![]() 即
即![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
函数![]() 在
在![]() 上不单调,不符合题目要求.
上不单调,不符合题目要求.
综上,若![]() 在
在![]() 上是单调函数,则
上是单调函数,则![]() 取唯一值:
取唯一值:![]() .
.
(2)解法一:已知“对![]() ,
,![]() 均成立”,
均成立”,
取![]() 得
得![]() ,
,
则![]() ,
,![]() ,则
,则![]() 时,
时,![]() ,
,![]() 在
在![]() 上增,
上增,
“对![]() ,
,![]() 均成立”等价于
均成立”等价于![]() ,
,
![]() ,
,
与![]() 取交集,得
取交集,得![]() ,
,
所以![]() 的取值范围是
的取值范围是![]()
解法二:根据(1),若![]() ,则
,则![]() 在
在![]() 上单减,
上单减,
“在区间![]() 上,
上,![]() 恒成立”等价于
恒成立”等价于![]()
![]() ,不成立;
,不成立;
若![]() 即
即![]() ,则
,则![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单减,
上单减,
在区间![]() 上,
上,![]() ,“在区间
,“在区间![]() 上,
上,![]() 恒成立”不成立;
恒成立”不成立;
若![]() 即
即![]() ,则
,则![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单增,
上单增,
在区间![]() 上,
上,![]() ,
,
“在区间![]() 上,
上,![]() 恒成立”
恒成立” ![]()
![]() ,
,
解得![]() ,与
,与![]() 相交取交集,得
相交取交集,得![]() ;
;
若![]() 即
即![]() ,则
,则![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
在区间![]() 上,
上,![]() ,
,
“在区间![]() 上,
上,![]() 恒成立”
恒成立”![]()
![]() .
.
设![]() ,
,
则![]() ,
,![]() 在
在![]() 上递增,
上递增,![]() ,
,
则函数![]() 在
在![]() 上递增,
上递增,![]() ,
,
因此![]() 时,
时,![]()
![]() 均不成立.
均不成立.
综上,所求![]() 的取值范围是
的取值范围是![]()

【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为了研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组: ![]() ,分别加以统计,得到如图所示的频率分布直方图.
,分别加以统计,得到如图所示的频率分布直方图.

(1)根据“25周岁以上组”的频率分布直方图,求25周岁以上组工人日平均生产件数的中位数的估计值(四舍五入保留整数);
(2)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(3)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“生产能手与工人所在年龄组有关”?
的把握认为“生产能手与工人所在年龄组有关”?
生产能手 | 非生产能手 | 合计 | |
25周岁以上组 | |||
25周岁以下组 | |||
合计 |
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
附: 
【题目】某城市先后采用甲、乙两种方案治理空气污染各一年,各自随机抽取一年(365天)内100天的空气质量指数API的检测数据进行分析,若空气质量指数值在[0,300]内为合格,否则为不合格.表1是甲方案检测数据样本的频数分布表,如图是乙方案检测数据样本的频率分布直方图.
表1:
API值 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | 大于300 |
天数 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
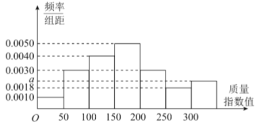
(1)将频率视为概率,求乙方案样本的频率分布直方图中![]() 的值,以及乙方案样本的空气质量不合格天数;
的值,以及乙方案样本的空气质量不合格天数;
(2)求乙方案样木的中位数;
(3)填写下面2×2列联表(如表2),并根据列联表判断是否有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.
表2:
甲方案 | 乙方案 | 合计 | |
合格天数 | _______ | _______ | _______ |
不合格天数 | _______ | _______ | _______ |
合计 | _______ | _______ | _______ |
附: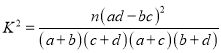
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |