题目内容
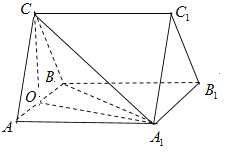
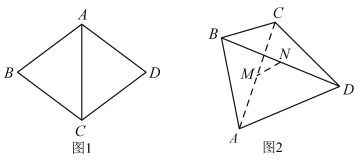
【题目】如图1.四边形![]() 是边长为10的菱形,其对角线
是边长为10的菱形,其对角线![]() ,现将
,现将![]() 沿对角线
沿对角线![]() 折起,连接
折起,连接![]() ,形成如图2的四面体
,形成如图2的四面体![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的大小为______.在图2中,设棱
所成角的大小为______.在图2中,设棱![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,若四面体
,若四面体![]() 的外接球的球心在四面体的内部,则线段
的外接球的球心在四面体的内部,则线段![]() 长度的取值范围为______.
长度的取值范围为______.
【答案】![]()
![]()
【解析】
连接![]() 、
、![]() ,利用线面垂直的判定定理可求异面直线
,利用线面垂直的判定定理可求异面直线![]() 与
与![]() 所成角的大小;先根据外接球的性质确定出四面体
所成角的大小;先根据外接球的性质确定出四面体![]() 的外接球球心,利用勾股定理,求出
的外接球球心,利用勾股定理,求出![]() 和
和![]() ,进而求出
,进而求出![]() ,借助三角函数的取值范围以及
,借助三角函数的取值范围以及![]() ,即可求出线段
,即可求出线段![]() 长度的取值范围.
长度的取值范围.
连接![]() 、
、![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() 为棱
为棱![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,
又![]() ,
,
则![]() 平面
平面![]() ,
,
由![]() 平面
平面![]() ,
,
则![]() ,即异面直线
,即异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
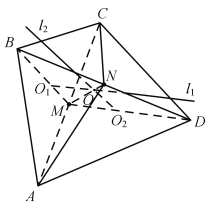
由四边形![]() 是边长为10的菱形,其对角线
是边长为10的菱形,其对角线![]() ,
,
则![]() ,
,![]() ,
,
![]() 是
是![]() 的外心,在中线
的外心,在中线![]() 中,
中,
设过点![]() 的直线
的直线![]() 平面
平面![]() ,易知
,易知![]() 平面
平面![]() ,
,
同理![]() 是
是![]() 的外心,在中线
的外心,在中线![]() 上,
上,
设过点![]() 的直线
的直线![]() 平面
平面![]() ,易知
,易知![]() 平面
平面![]() ,
,
由对称性易知![]() 、
、![]() 的交点
的交点![]() 在直线
在直线![]() 上,
上,
根据外接球的性质,点![]() 为四面体
为四面体![]() 的外接球的球心,
的外接球的球心,
![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
令![]() ,根据题意可知
,根据题意可知![]() ,
,![]() ,且
,且![]() ,
,
则![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
![]() ,即线段
,即线段![]() 长度的取值范围为
长度的取值范围为![]() ,
,
故答案为:![]() ;
;![]()

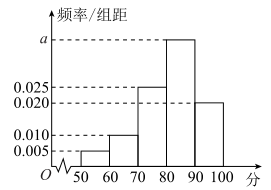
【题目】某城市先后采用甲、乙两种方案治理空气污染各一年,各自随机抽取一年(365天)内100天的空气质量指数API的检测数据进行分析,若空气质量指数值在[0,300]内为合格,否则为不合格.表1是甲方案检测数据样本的频数分布表,如图是乙方案检测数据样本的频率分布直方图.
表1:
API值 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | 大于300 |
天数 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
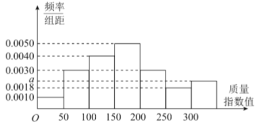
(1)将频率视为概率,求乙方案样本的频率分布直方图中![]() 的值,以及乙方案样本的空气质量不合格天数;
的值,以及乙方案样本的空气质量不合格天数;
(2)求乙方案样木的中位数;
(3)填写下面2×2列联表(如表2),并根据列联表判断是否有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.
表2:
甲方案 | 乙方案 | 合计 | |
合格天数 | _______ | _______ | _______ |
不合格天数 | _______ | _______ | _______ |
合计 | _______ | _______ | _______ |
附: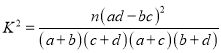
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |