题目内容
【题目】已知函数![]()
(1)若![]() ,试讨论
,试讨论![]() 的单调性;
的单调性;
(2)若![]() ,实数
,实数![]() 为方程
为方程![]() 的两不等实根,求证:
的两不等实根,求证:![]() .
.
【答案】(1)答案不唯一,具体见解析(2)证明见解析
【解析】
(1)根据题意得![]() ,分
,分![]() 与
与![]() 讨论即可得到函数
讨论即可得到函数![]() 的单调性;
的单调性;
(2)根据题意构造函数![]() ,得
,得![]() ,参变分离得
,参变分离得![]() ,
,
分析不等式![]() ,即转化为
,即转化为![]() ,设
,设![]() ,再构造函数
,再构造函数![]() ,利用导数得单调性,进而得证.
,利用导数得单调性,进而得证.
(1)依题意![]() ,当
,当![]() 时,
时,![]() ,
,
①当![]() 时,
时,![]() 恒成立,此时
恒成立,此时![]() 在定义域上单调递增;
在定义域上单调递增;
②当![]() 时,若
时,若![]() ,
,![]() ;若
;若![]() ,
,![]() ;
;
故此时![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)方法1:由![]() 得
得![]()
令![]() ,则
,则![]() ,
,
依题意有![]() ,即
,即![]() ,
,
要证![]() ,只需证
,只需证![]() (不妨设
(不妨设![]() ),
),
即证![]() ,
,
令![]() ,设
,设![]() ,则
,则![]() ,
,
![]() 在
在![]() 单调递减,即
单调递减,即![]() ,从而有
,从而有![]() .
.
方法2:由![]() 得
得![]()
令![]() ,则
,则![]() ,
,![]()
当![]() 时
时![]() ,
,![]() 时
时![]() ,
,
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
不妨设![]() ,则
,则![]() ,
,
要证![]() ,只需证
,只需证![]() ,易知
,易知![]() ,
,
故只需证![]() ,即证
,即证![]()
令![]() ,(
,(![]() ),
),
则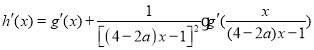
= =
=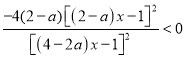 ,
,
(也可代入后再求导)
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
故对于![]() 时,总有
时,总有![]() .由此得
.由此得![]()

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
【题目】为认真贯彻落实党中央国务院决策部署,坚持“房子是用来住的,不是用来炒的”定位,坚持调控政策的连续性和稳定性,进一步稳定某省市商品住房市场,该市人民政府办公厅出台了相关文件来控制房价,并取得了一定效果,下表是2019年2月至6月以来该市某城区的房价均值数据:
| 2 | 3 | 4 | 5 | 6 |
| 9.80 | 9.70 |
| 9.30 | 9.20 |
已知:![]() .
.![]()
(1)若变量![]() 、
、![]() 具有线性相关关系,求房价均价
具有线性相关关系,求房价均价![]() (千元/平方米)关于月份
(千元/平方米)关于月份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测该市某城区7月份的房价.
(参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式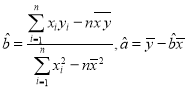 )
)