题目内容
【题目】已知椭圆C：
（
）经过
，
两点.O为坐标原点，且
的面积为
.过点
且斜率为k（
）的直线l与椭圆C有两个不同的交点M，N，且直线
，
分别与y轴交于点S，T.
（Ⅰ）求椭圆C的方程；
（Ⅱ）求直线l的斜率k的取值范围；
（Ⅲ）设
，
，求
的取值范围.
【答案】（Ⅰ）
（Ⅱ）
（Ⅲ）
【解析】
（Ⅰ）把点A坐标代入椭圆的方程得
.由
的面积为
可知，
，解得b，进而得椭圆C的方程.
（Ⅱ）设直线l的方程为
，
，
.联立直线l与椭圆C的方程可得关于x的一元二次方程.
，进而解得k的取值范围.
（Ⅲ）因为
，
，，，写出直线
的方程，令
，解得
.点S的坐标为
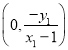.同理可得：点T的坐标为
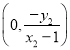.用坐标表示
，
，
，代入
，
，得
.同理
.由（Ⅱ）得
，
，代入
，化简再求取值范围.
（Ⅰ）因为椭圆C：
经过点，
所以
解得.
由的面积为可知，，
解得
，
所以椭圆C的方程为.
（Ⅱ）设直线l的方程为，，.
联立
，消y整理可得：
.
因为直线与椭圆有两个不同的交点，
所以
，解得
.
因为
，所以k的取值范围是.
（Ⅲ）因为，，，.
所以直线的方程是：
.
令，解得.
所以点S的坐标为.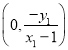
同理可得：点T的坐标为.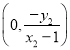
所以
，
，
.
由，，
可得：
，
，
所以.
同理.
由（Ⅱ）得，，
所以
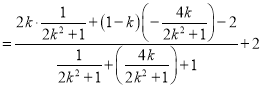
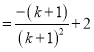
所以的范围是.
【题目】BMI指数（身体质量指数，英文为BodyMassIndex，简称BMI）是衡量人体胖瘦程度的一个标准，BMI=体重（kg）/身高（m）的平方.根据中国肥胖问题工作组标准，当BMI≥28时为肥胖.某地区随机调查了1200名35岁以上成人的身体健康状况，其中有200名高血压患者，被调查者的频率分布直方图如下：
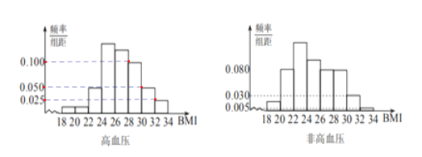
（1）求被调查者中肥胖人群的BMI平均值
；
（2）填写下面列联表，并判断是否有99.9%的把握认为35岁以上成人患高血压与肥胖有关.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合计 | |
高血压 | |||
非高血压 | |||
合计 |
附：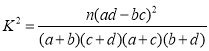
，
【题目】某城市先后采用甲、乙两种方案治理空气污染各一年，各自随机抽取一年（365天）内100天的空气质量指数API的检测数据进行分析，若空气质量指数值在[0，300]内为合格，否则为不合格.表1是甲方案检测数据样本的频数分布表，如图是乙方案检测数据样本的频率分布直方图.
表1：
API值 | [0，50] | （50，100] | （100，150] | （150，200] | （200，250] | （250，300] | 大于300 |
天数 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
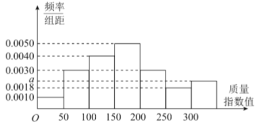
（1）将频率视为概率，求乙方案样本的频率分布直方图中
的值，以及乙方案样本的空气质量不合格天数；
（2）求乙方案样木的中位数；
（3）填写下面2×2列联表（如表2），并根据列联表判断是否有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.
表2：
甲方案 | 乙方案 | 合计 | |
合格天数 | _______ | _______ | _______ |
不合格天数 | _______ | _______ | _______ |
合计 | _______ | _______ | _______ |
附：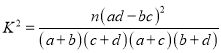
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
