题目内容
19.已知等差数列{an}的各项均为正数,a1=3,其前n项和为Sn,数列{bn}为等比数列,且b1=1,b2S2=16,b3S3=60.求:(Ⅰ)数列{an}与{bn}的通项公式;
(Ⅱ)$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$.
分析 (I)利用等差数列与等比数列的通项公式即可得出;
(Ⅱ)由Sn=n(n+2),可得$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$.利用“裂项求和”即可得出.
解答 解:(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q,则d>0,
an=3+(n-1)d,bn=qn-1.
∵b2S2=16,b3S3=60.
∴$\left\{\begin{array}{l}{(6+d)q=16}\\{(9+3){q}^{2}=60}\end{array}\right.$,
解得$\left\{\begin{array}{l}{d=2}\\{q=2}\end{array}\right.$或$\left\{\begin{array}{l}{d=-\frac{6}{5}}\\{q=\frac{10}{3}}\end{array}\right.$(舍去).
故an=3+2(n-1)=2n+1,${b}_{n}={2}^{n-1}$.
(Ⅱ)∵Sn=$\frac{n(3+2n+1)}{2}$=n(n+2),
∴$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$.
∴$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})+(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{n(3n+5)}{4(n+1)(n+2)}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | $\frac{1}{12}$ | B. | 12 | C. | $-\frac{1}{12}$ | D. | -12 |
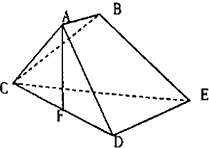 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.