题目内容
2.已知函数f(x)=$\frac{1}{2}$x2-x-2lnx,则函数f(x)的单调递增区间为( )| A. | (-∞,-1)(2,+∞) | B. | (2,+∞) | C. | (-∞,-1) | D. | (-1,2) |
分析 先求函数的定义域,再求导数,令导数大于0,解得x的范围即为函数的单调增区间.
解答 解:函数f(x)=$\frac{1}{2}$x2-x-2lnx,的定义域为(0,+∞)
对函数f(x)=$\frac{1}{2}$x2-x-2lnx,求导,得f′(x)=x-1-$\frac{2}{x}$,
令f′(x)>0,∵x>0,∴得x-1-$\frac{2}{x}$>0,解得,x>2.
∴函数的单调增区间为(2,+∞).
故选:B.
点评 本题主要考查利用导数求函数的单调区间,易错点是忘记求函数的定义域.

练习册系列答案
相关题目
8.将函数f(x)=cos2x(x∈R)的图象沿向量$\overrightarrow{a}$平移后,所得曲线对应的函数在区间[$\frac{π}{3}$,$\frac{2π}{3}$]内单调递增,且在该区间的最大值为1,则向量$\overrightarrow{a}$可能是( )
| A. | (-$\frac{π}{6}$,$\frac{1}{2}$) | B. | ($\frac{π}{6}$,$\frac{1}{2}$) | C. | ($\frac{π}{3}$,$\frac{3}{2}$) | D. | (-$\frac{π}{3}$,$\frac{3}{2}$) |
13.若椭圆的长轴长、短轴长、焦距组成一个等差数列,则该椭圆的离心率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12.观察下列顺序排列的等式:9×0+1=1;9×1+2=11;9×2+3=21;9×3+4=31…猜想第n个等式应为( )
| A. | 9(n+1)+n=10n+9 | B. | 9(n-1)+(n-1)=10n-10 | C. | 9n+(n-1)=10n-1 | D. | 9(n-1)+n=10n-9 |
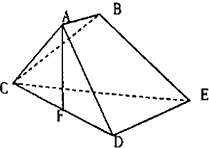 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.