题目内容
设P为椭圆 =1(a>b>0)上任一点,F1、F2分别为左、右焦点,求|PF1|·|PF2|的最大、最小值.
=1(a>b>0)上任一点,F1、F2分别为左、右焦点,求|PF1|·|PF2|的最大、最小值.
 =1(a>b>0)上任一点,F1、F2分别为左、右焦点,求|PF1|·|PF2|的最大、最小值.
=1(a>b>0)上任一点,F1、F2分别为左、右焦点,求|PF1|·|PF2|的最大、最小值.当x02=0,即x0=0时,z最大=a2;
当x0=±a,x02=a2时,z最小=a2-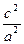 ·a2=a2-c2=b2.
·a2=a2-c2=b2.
当x0=±a,x02=a2时,z最小=a2-
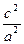 ·a2=a2-c2=b2.
·a2=a2-c2=b2.解法一:令z=|PF1|·|PF2|=(a+ex0)(a-ex0)=a2-e2x02.
∵-a≤x0≤a,∴0≤x02≤a2.
当x02=0,即x0=0时,z最大=a2;
当x0=±a,x02=a2时,z最小=a2-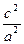 ·a2=a2-c2=b2.
·a2=a2-c2=b2.
解法二:∵|PF1|+|PF2|=2a,∴|PF1|·|PF2|≤( )2=a2,
)2=a2,
当且仅当|PF1|=|PF2|时,取“=”.∴z最大=a2.求z最小同上.
∵-a≤x0≤a,∴0≤x02≤a2.
当x02=0,即x0=0时,z最大=a2;
当x0=±a,x02=a2时,z最小=a2-
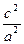 ·a2=a2-c2=b2.
·a2=a2-c2=b2.解法二:∵|PF1|+|PF2|=2a,∴|PF1|·|PF2|≤(
 )2=a2,
)2=a2,当且仅当|PF1|=|PF2|时,取“=”.∴z最大=a2.求z最小同上.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
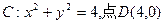 ,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量
,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量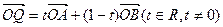 .
.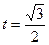 时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标.
时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标.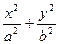 =1(a>b>0)的内接矩形面积的最大值.
=1(a>b>0)的内接矩形面积的最大值. ;
; ;
; .
.

 -
-
 ,且过点(2,0)的椭圆的标准方程为( )
,且过点(2,0)的椭圆的标准方程为( ) +y2=1或
+y2=1或 +
+ ="1"
="1" =1
=1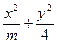 =1的焦距为2,则m的值等于__________________.
=1的焦距为2,则m的值等于__________________. 的椭圆
的椭圆 过点
过点 ,
, 是坐标原点.
是坐标原点. 的方程;
的方程; 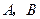 为椭圆
为椭圆 ,判定直线
,判定直线 与圆
与圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. =1的准线平行于x轴,则实数m的取值范围是( )
=1的准线平行于x轴,则实数m的取值范围是( ) <m<3且m≠0
<m<3且m≠0