题目内容
【题目】在直角坐标系xOy中，直线l的参数方程为 
（t为参数），以原点O为极点，x轴的非负半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=2 
sinθ．
（1）求圆C的直角做标方程；
（2）圆C的圆心为C，点P为直线l上的动点，求|PC|的最小值．
【答案】
（1）解：由圆C的极坐标方程ρ=2 
sinθ，可得：ρ2=2 ρsinθ．
由ρ2=x2+y2，y=ρsinθ代入可得： 
．
即圆的方程为： 
．
（2）解：由直线l的参数方程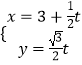 
（t为参数），消去参数t，可得： 
．
由（1）可得：圆心为（0， ），半径
圆心到直线的距离d= 
= 
．
∵|PC|的最小值等于圆心到直线的d减去半径r．
所以：|PC|的最小值 
【解析】（1）由ρ2=x2+y2 ， x=ρcosθ，y=ρsinθ，代入即可得圆C的直角坐标方程．（2）把直线化成直角坐标方程，直线到圆上的距离最小，即是圆心到直线的d减去半径r．
练习册系列答案
相关题目
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x（年） | 0 | 1 | 2 | 3 | 4 |
人口数y（十万） | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据，求出y关于x的线性回归方程；
(2) 据此估计2015年该城市人口总数。
