题目内容
【题目】某跳水运动员在一次跳水训练时的跳水曲线为如图所示抛物线的一段.已知跳水板![]() 长为
长为![]() ,跳水板距水面
,跳水板距水面![]() 的高
的高![]() 为
为![]() .为安全和空中姿态优美,训练时跳水曲线应在离起跳点
.为安全和空中姿态优美,训练时跳水曲线应在离起跳点![]() 处水平距
处水平距![]()
![]() 时达到距水面最大高度
时达到距水面最大高度![]() ,规定:以
,规定:以![]() 为横轴,
为横轴,![]() 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.
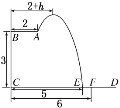
(1)当![]() 时,求跳水曲线所在的抛物线方程;
时,求跳水曲线所在的抛物线方程;
(2)若跳水运动员在区域![]() 内入水时才能达到比较好的训练效果,求此时
内入水时才能达到比较好的训练效果,求此时![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1) 题中已经规定了直角坐标系,我们能获取到抛物线顶点坐标![]() ,这样一来我们可以设该抛物线的顶点式
,这样一来我们可以设该抛物线的顶点式![]() ,又抛物线过点
,又抛物线过点![]() 代入前面的表达式,求出抛物线方程.
代入前面的表达式,求出抛物线方程.
(2) 由顶点坐标最高点为![]() ,
,![]() .设抛物线方程为
.设抛物线方程为![]() .又过点
.又过点![]() ,代入抛物线方程得到
,代入抛物线方程得到![]() ,又跳水运动员要跳入区域
,又跳水运动员要跳入区域![]() ,转化
,转化![]() 在区间
在区间![]() 内有一解,再根据二次函数零点分布知识点,可以得到相应不等式
内有一解,再根据二次函数零点分布知识点,可以得到相应不等式 .求出h的取值范围.
.求出h的取值范围.
由题意,最高点为![]() ,
,![]() .设抛物线方程为
.设抛物线方程为![]() .
.
(1)当![]() 时,最高点为
时,最高点为![]() ,方程为
,方程为![]()
将点![]() 代入
代入![]() 式得
式得![]() .即所求抛物线的方程为
.即所求抛物线的方程为![]() .
.
(2)将点![]() 代入
代入![]() ,得
,得![]() .
.
由题意,方程![]() 在区间
在区间![]() 内有一解.
内有一解.
令![]() ,
,
则 ,解得
,解得![]() .
.
答:达到比较好的训练效果时的h的取值范围是![]() .
.


练习册系列答案
相关题目