题目内容
【题目】已知f(x)是定义在R上的增函数,函数y=f(x﹣1)的图象关于点(1,0)对称,若对任意的x,y∈R,等式f(y﹣3)+f( ![]() )=0恒成立,则
)=0恒成立,则 ![]() 的取值范围是( )
的取值范围是( )
A.[2﹣ ![]()
![]() ,2+
,2+ ![]()
![]() ]
]
B.[1,2+ ![]()
![]() ]
]
C.[2﹣ ![]()
![]() ,3]
,3]
D.[1,3]
【答案】C
【解析】解:函数y=f(x)的图象可由y=f(x﹣1)的图象向左平移1个单位得到,
由于y=f(x﹣1)的图象关于点(1,0)对称,
则y=f(x)的图象关于原点对称,
则f(x)为奇函数,即有f(﹣x)=﹣f(x),
则等式f(y﹣3)+f( ![]() )=0恒成立即为
)=0恒成立即为
f(y﹣3)=﹣f( ![]() )=f(﹣
)=f(﹣ ![]() ),
),
又f(x)是定义在R上的增函数,则有y﹣3=﹣ ![]() ,
,
两边平方可得,(x﹣2)2+(y﹣3)2=1,
即有y=3﹣ ![]() 为以(2,3)为圆心,1为半径的下半圆,
为以(2,3)为圆心,1为半径的下半圆,
则 ![]() =
= ![]() 可看作是半圆上的点与原点的连线的斜率,
可看作是半圆上的点与原点的连线的斜率,
如图,kOA= ![]() =3,取得最大,过O作切线OB,设OB:y=kx,
=3,取得最大,过O作切线OB,设OB:y=kx,
则由d=r得, ![]() =1,解得,k=2
=1,解得,k=2 ![]() ,
,
由于切点在下半圆,则取k=2﹣ ![]() ,即为最小值.
,即为最小值.
则 ![]() 的取值范围是[2﹣
的取值范围是[2﹣ ![]() ,3].
,3].
故选C.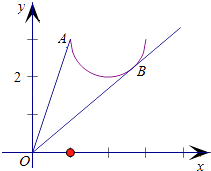
【考点精析】解答此题的关键在于理解函数单调性的性质的相关知识,掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集.

【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合计 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”,按分层抽样的方法,在我市所有“移动支付达人”中,随机抽取6名用户
求抽取的6名用户中,男女用户各多少人;
② 从这6名用户中抽取2人,求既有男“移动支付达人”又有女“移动支付达人”的概率.
(2)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,填写下表,问能否在犯错误概率不超过0.01的前提下,认为“移动支付活跃用户”与性别有关?
P(χ2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | .635 |

非移动支付活跃用户 | 移动支付活跃用户 | 合计 | |
男 | |||
女 | |||
合计 |
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 6 | ||
女生 | 10 | ||
合计 | 48 |
已知在全班48人中随机抽取1人,抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的2×2列联表补充完整;(不用写计算过程)
(2)能否在犯错误的概率不超过0.05的前提下认为喜爱打篮球与性别有关?说明你的理由.
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)


