题目内容
【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别是棱A1B1 , B1C1的中点,O是AC与BD的交点,面OEF与面BCC1B1相交于m,面OD1E与面BCC1B1相交于n,则直线m,n的夹角为( )
A.0
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:如图所示: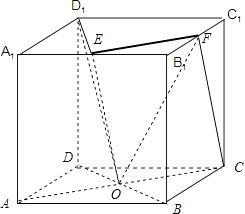
∵E,F分别是棱A1B1 , B1C1的中点,
故EF∥AC,
则面OEF即平面EFCA与面BCC1B1相交于CF,即直线m,
由CF∥OE,可得CF∥平面OD1E,
故面OD1E与面BCC1B1相交于n时,
必有n∥CF,即n∥m,
即直线m,n的夹角为0,
故选:A
【考点精析】根据题目的已知条件,利用异面直线及其所成的角和空间中直线与直线之间的位置关系的相关知识可以得到问题的答案,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

练习册系列答案
相关题目