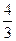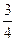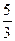题目内容
已知 中,
中,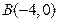 ,
,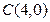 ,
,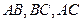 成等差数列,求点
成等差数列,求点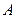 的轨迹。
的轨迹。
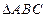 中,
中,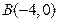 ,
,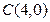 ,
,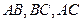 成等差数列,求点
成等差数列,求点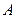 的轨迹。
的轨迹。点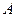 的轨迹是一个以
的轨迹是一个以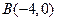 ,
,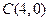 为焦点的椭圆,但要去除掉两个点
为焦点的椭圆,但要去除掉两个点
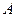 的轨迹是一个以
的轨迹是一个以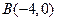 ,
,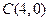 为焦点的椭圆,但要去除掉两个点
为焦点的椭圆,但要去除掉两个点∵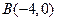 ,
,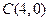 且
且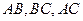 成等差数列,∴
成等差数列,∴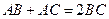 ,又∵
,又∵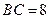 ,∴
,∴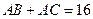 ,即点
,即点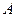 到两定点
到两定点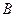 和
和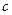 的距离之和为一定值,且这个定值大于
的距离之和为一定值,且这个定值大于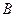 和
和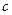 的距离,∴根据椭圆的定义,点
的距离,∴根据椭圆的定义,点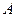 的轨迹是一个椭圆,但是由于当
的轨迹是一个椭圆,但是由于当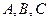 三点在一条直线上时,不能构成三角形,∴点
三点在一条直线上时,不能构成三角形,∴点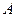 的轨迹是一个以
的轨迹是一个以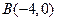 ,
,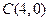 为焦点的椭圆,但要去除掉两个点。
为焦点的椭圆,但要去除掉两个点。
名师点金:原题是证明点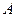 在椭圆上运动,而变式是求点
在椭圆上运动,而变式是求点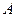 的轨迹,两者解法一致,均采用设点
的轨迹,两者解法一致,均采用设点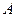 的坐标后利用圆锥曲线的定义得到
的坐标后利用圆锥曲线的定义得到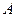 点的轨迹为一椭圆,两者只是在题型上有所区别。
点的轨迹为一椭圆,两者只是在题型上有所区别。
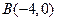 ,
,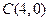 且
且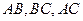 成等差数列,∴
成等差数列,∴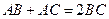 ,又∵
,又∵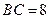 ,∴
,∴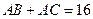 ,即点
,即点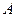 到两定点
到两定点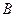 和
和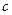 的距离之和为一定值,且这个定值大于
的距离之和为一定值,且这个定值大于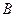 和
和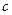 的距离,∴根据椭圆的定义,点
的距离,∴根据椭圆的定义,点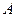 的轨迹是一个椭圆,但是由于当
的轨迹是一个椭圆,但是由于当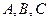 三点在一条直线上时,不能构成三角形,∴点
三点在一条直线上时,不能构成三角形,∴点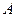 的轨迹是一个以
的轨迹是一个以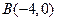 ,
,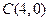 为焦点的椭圆,但要去除掉两个点。
为焦点的椭圆,但要去除掉两个点。名师点金:原题是证明点
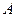 在椭圆上运动,而变式是求点
在椭圆上运动,而变式是求点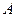 的轨迹,两者解法一致,均采用设点
的轨迹,两者解法一致,均采用设点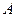 的坐标后利用圆锥曲线的定义得到
的坐标后利用圆锥曲线的定义得到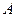 点的轨迹为一椭圆,两者只是在题型上有所区别。
点的轨迹为一椭圆,两者只是在题型上有所区别。
练习册系列答案
相关题目
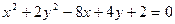
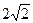
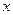 轴上,离心率
轴上,离心率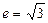 ,焦距为
,焦距为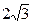
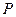
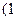 ,
,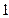 )的直线
)的直线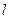 与该双曲线交于
与该双曲线交于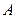 ,
,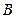 两点,且点
两点,且点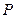 是线段
是线段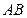 的中点?若存在,请求出直线
的中点?若存在,请求出直线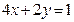 ;②
;②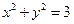 ;③
;③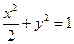 ;④
;④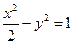 。其中与直线
。其中与直线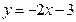 有交点的所有曲线是( )
有交点的所有曲线是( )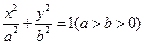 的左焦点为F,上顶点为A,直线
的左焦点为F,上顶点为A,直线 AF的倾斜角为
AF的倾斜角为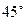 (1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线
(1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线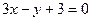 相切,求椭圆的方程及圆M的方程
相切,求椭圆的方程及圆M的方程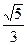 ,短轴长为4,求椭圆标准方程
,短轴长为4,求椭圆标准方程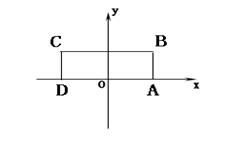
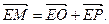 (Ⅰ)求点M的轨迹方程;
(Ⅰ)求点M的轨迹方程;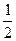 ),过点F的直线l与点M的轨迹相交于Q、R两点,且
),过点F的直线l与点M的轨迹相交于Q、R两点,且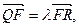 求实数
求实数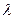 的取值范围.
的取值范围.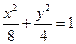 有相同的焦点,直线y=
有相同的焦点,直线y=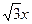 为C的一条渐近线. 过点P(0,4)的直线
为C的一条渐近线. 过点P(0,4)的直线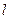 ,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当
,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当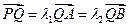 ,且
,且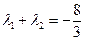 时,求Q点的坐标.
时,求Q点的坐标.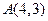 ,点
,点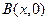 在
在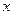 轴正半轴上移动,
轴正半轴上移动,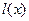 表示
表示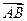 的长,则△ABC中两边长的比值
的长,则△ABC中两边长的比值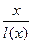 的最大值为
的最大值为