题目内容
16.已知函数f′(x)=$\frac{a}{x}-2bx({x>0})$是函数f(x)的导数,且函数f′(x)图象上一点P(2,f′(2))处的切线方程为5x+2y-4=0(1)求a,b的值;
(2)若方程xf′(x)+x2+2lnx+m=0在区间$[{\frac{1}{e},e}]$上有两个不等实数根,求实数m的取值范围
(3)令g(x)=f(x)-nx(n∈R),如果g(x)的图象与x轴交于A(x1,0),B(x2,0)(x1<x2)两点,AB的中点为C(x0,0),求证:g′(x0)≠0.
分析 (1)求得函数f′(x)的导数,求得切线的斜率,由切线方程,可得切点和斜率,解方程可得a,b;
(2)方程xf′(x)+x2+2lnx+m=0即为2lnx-x2+m+2=0,令g(x)=2lnx-x2+m+2,求出导数,求得单调区间和极值、最值,即可得到实数m的取值范围;
(3)由函数g(x)的图象与x轴交于两个不同的点A(x1,0),B(x2,0),2lnx-x2-nx+c=0的两个根为x1,x2,知$\left\{\begin{array}{l}{2ln{x}_{1}-{{x}_{1}}^{2}-n{x}_{1}+c=0}\\{2ln{x}_{2}-{{x}_{2}}^{2}-n{x}_{2}+c=0}\end{array}\right.$,两式相减,令t=$\frac{{x}_{1}}{{x}_{2}}$,0<t<1,构造函数u(t)=$\frac{2(1-t)}{1+t}$+lnt,证明u(t)<0在0<t<1上恒成立,由此能够证明g′(x0)≠0.
解答 解:(1)函数f′(x)=$\frac{a}{x}-2bx({x>0})$的导数为-2b-$\frac{a}{{x}^{2}}$,
图象上一点P(2,f′(2))处切线的斜率为-2b-$\frac{a}{4}$=-$\frac{5}{2}$,
f′(2)=$\frac{1}{2}$a-4b=-3,
解方程可得a=2,b=1;
(2)方程xf′(x)+x2+2lnx+m=0即为
2lnx-x2+m+2=0,
令g(x)=2lnx-x2+m+2,
则g′(x)=$\frac{2}{x}$-2x=$\frac{-2(x+1)(x-1)}{x}$,
∵x∈[$\frac{1}{e}$,e],∴g′(x)=0时,x=1.
当$\frac{1}{e}$<x<1时,g′(x)>0;
当1<x<e时,g′(x)<0,
故函数g(x)在x=1取得最大值g(1)=m+1,
又g($\frac{1}{e}$)=m-$\frac{1}{{e}^{2}}$,g(e)=m+4-e2,
g(e)-g($\frac{1}{e}$)=4-e2+$\frac{1}{{e}^{2}}$<0,
则g(e)<g($\frac{1}{e}$),
故函数g(x)在[$\frac{1}{e}$,e]上的最小值是g(e).
方程xf′(x)+x2+2lnx+m=0在[$\frac{1}{e}$,e]上有两个不相等的实数根,
则有$\left\{\begin{array}{l}{g(1)=m+1>0}\\{g(\frac{1}{e})=m-\frac{1}{{e}^{2}}≤0}\end{array}\right.$,
解得-1<m≤$\frac{1}{{e}^{2}}$,
故实数m的取值范围是(-1,$\frac{1}{{e}^{2}}$];
(3)∵函数g(x)的图象与x轴交于两个不同的点A(x1,0),B(x2,0),
2lnx-x2-nx+c=0的两个根为x1,x2,
则$\left\{\begin{array}{l}{2ln{x}_{1}-{{x}_{1}}^{2}-n{x}_{1}+c=0}\\{2ln{x}_{2}-{{x}_{2}}^{2}-n{x}_{2}+c=0}\end{array}\right.$,
两式相减,得n=-(x1+x2)+$\frac{2(ln{x}_{1}-ln{x}_{2})}{{x}_{1}-{x}_{2}}$,
g(x)=2lnx-x2-nx+c,
g′(x)=$\frac{2}{x}$-2x-n,
则g′(x0)=g′($\frac{1}{2}$x1+$\frac{1}{2}$x2)=$\frac{4}{{x}_{1}+{x}_{2}}$-(x1+x2)+(x1+x2)-$\frac{2(ln{x}_{1}-ln{x}_{2})}{{x}_{1}-{x}_{2}}$,
=$\frac{4}{{x}_{1}+{x}_{2}}$-$\frac{2(ln{x}_{1}-ln{x}_{2})}{{x}_{1}-{x}_{2}}$,
下面证明$\frac{4}{{x}_{1}+{x}_{2}}$-$\frac{2(ln{x}_{1}-ln{x}_{2})}{{x}_{1}-{x}_{2}}$<0,(0<x1<x2)
即证明$\frac{2({x}_{2}-{x}_{1})}{{x}_{2}+{x}_{1}}$+ln$\frac{{x}_{1}}{{x}_{2}}$<0,
令t=$\frac{{x}_{1}}{{x}_{2}}$,∵0<x1<x2,∴0<t<1,
即证明u(t)=$\frac{2(1-t)}{1+t}$+lnt<0在0<t<1上恒成立.
由u′(t)=$\frac{1}{t}$-$\frac{4}{(1+t)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$
∵0<t<1,∴u′(t)>0,
∴u(t)在(0,1)上是增函数,
则u(t)<u(1)=0,
∴$\frac{2({x}_{2}-{x}_{1})}{{x}_{2}+{x}_{1}}$+ln$\frac{{x}_{1}}{{x}_{2}}$<0,
故g′(x0)<0,
所以g′(x0)≠0.
点评 本题考查切线方程的运用,考查满足条件的实数的取值范围的求法,考查不等式的证明.解题时要认真审题,注意导数性质的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
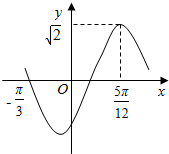 函数f(x)=$\sqrt{2}$sin(ωx+θ)(x∈R,ω>0,|θ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递减区间为( )
函数f(x)=$\sqrt{2}$sin(ωx+θ)(x∈R,ω>0,|θ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递减区间为( )| A. | $[\frac{5π}{12}+kπ,\frac{11π}{12}+kπ],k∈z$ | B. | $[\frac{5π}{6}+kπ≤x≤\frac{11π}{6}+kπ],k∈z$ | ||
| C. | $[\frac{5π}{12}+2kπ,\frac{11π}{12}+2kπ],k∈z$ | D. | $[-\frac{π}{12}+kπ,\frac{5π}{12}+kπ],k∈z$ |
| A. | |a7|>|a8| | B. | |a7|<|a8| | C. | |a8|=|a7| | D. | a7=0 |
| A. | $({0,\frac{1}{e}})$ | B. | $({\frac{1}{e},1})$ | C. | (1,e) | D. | (e,+∞) |