题目内容
6．已知P（x，y）为圆（x-2）2+y2=1上的动点，则|3x+4y-3|的最大值为8．分析 设t=3x+4y-3，由直线和圆相切可得t的范围，可得答案．
解答 解：设t=3x+4y-3，即3x+4y-3-t=0，
由圆心（2，0）到直线3x+4y-3-t=0的距离d=1可得：
$\frac{|6-3-t|}{\sqrt{{3}^{2}+{4}^{2}}}$=1，解得t=8或t=-2，
由题意可得-2≤t≤8，∴0≤|3x+4y-3|≤8，
故答案为：8．
点评 本题考查点和直线与圆的位置关系，属基础题．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
相关题目
17．若x∈（0，1），则下列结论正确的是（ ）
| A． | $lgx＞\sqrt{x}＞{2^x}$ | B． | ${2^x}＞lgx＞\sqrt{x}$ | C． | ${2^x}＞\sqrt{x}＞lgx$ | D． | $\sqrt{x}＞{2^x}＞lgx$ |
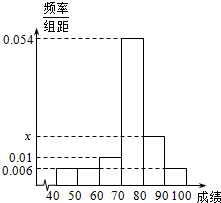某班50位学生2015届中考试数学成绩的频率直方分布图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．
15．已知复数$\frac{2a+i}{2i-1}$是纯虚数，则实数a=（ ）
| A． | -1 | B． | -$\frac{1}{4}$ | C． | $\frac{1}{4}$ | D． | 1 |