题目内容
5.在数列{an}中,an+1=can(c为非零常数),前n项和为Sn=3n+k,则实数k=-1.分析 可证数列{an}是以c为公比的等比数列,代入等比数列的求和公式比较系数可得.
解答 解:∵在数列{an}中,an+1=can(c为非零常数),
∴数列{an}是以c为公比的等比数列,
∴Sn=$\frac{{a}_{1}(1-{c}^{n})}{1-c}$=-$\frac{{a}_{1}}{1-c}$×cn+$\frac{{a}_{1}}{1-c}$=3n+k,
比较系数可得c=3且$\frac{{a}_{1}}{1-c}$=-1,即k=-1,
故答案为:-1.
点评 本题考查等比数列的求和公式,涉及等比数列的判定,属基础题.

练习册系列答案
相关题目
13.设M={2},N={2,3},则下列表示不正确的是( )
| A. | M?N | B. | M⊆N | C. | 2∈N | D. | 2?N |
17.若x∈(0,1),则下列结论正确的是( )
| A. | $lgx>\sqrt{x}>{2^x}$ | B. | ${2^x}>lgx>\sqrt{x}$ | C. | ${2^x}>\sqrt{x}>lgx$ | D. | $\sqrt{x}>{2^x}>lgx$ |
15.已知复数$\frac{2a+i}{2i-1}$是纯虚数,则实数a=( )
| A. | -1 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | 1 |
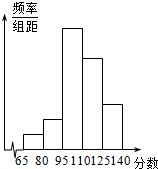 为了解某校高二学生联考数学成绩分布,从该校参加联科的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图,若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频率是6,则样本容量为40;众数为102.5.
为了解某校高二学生联考数学成绩分布,从该校参加联科的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图,若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频率是6,则样本容量为40;众数为102.5.