题目内容
1．函数f（x）=lnx+ex（e为自然对数的底数）的零点所在的区间是（ ）| A． | $（{0，\frac{1}{e}}）$ | B． | $（{\frac{1}{e}，1}）$ | C． | （1，e） | D． | （e，+∞） |
分析 函数f（x）=lnx+ex在（0，+∞）上单调递增，因此函数f（x）最多只有一个零点．再利用函数零点存在判定定理即可判断出．
解答 解：函数f（x）=lnx+ex在（0，+∞）上单调递增，因此函数f（x）最多只有一个零点．
当x→0+时，f（x）→-∞；又$f（\frac{1}{e}）$=$ln\frac{1}{e}$+${e}^{\frac{1}{e}}$=${e}^{\frac{1}{e}}$-1＞0，
∴函数f（x）=lnx+ex（e为自然对数的底数）的零点所在的区间是$（0，\frac{1}{e}）$．
故选：A．
点评 本题考查了函数零点存在判定定理、函数的单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
12．下列函数中，在其定义域内既是偶函数又在（-∞，0）上单调递增的函数是（ ）
| A． | f（x）=x2 | B． | f（x）=2|x| | C． | f（x）=log2$\frac{1}{|x|}$ | D． | f（x）=sinx |
9．某中学安排语文、数学、英语各一名教师负责期末考试的一个考场的语文、数学、英语的监考工作，每场考试需要两名教师，则每科目的考试恰有同科目的教师监考的概率为（ ）
| A． | $\frac{5}{9}$ | B． | $\frac{8}{27}$ | C． | $\frac{4}{27}$ | D． | $\frac{2}{9}$ |
13．设M={2}，N={2，3}，则下列表示不正确的是（ ）
| A． | M?N | B． | M⊆N | C． | 2∈N | D． | 2?N |
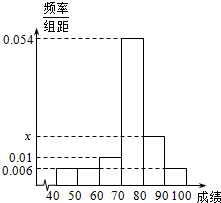某班50位学生2015届中考试数学成绩的频率直方分布图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．