题目内容
4.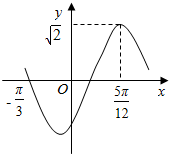 函数f(x)=$\sqrt{2}$sin(ωx+θ)(x∈R,ω>0,|θ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递减区间为( )
函数f(x)=$\sqrt{2}$sin(ωx+θ)(x∈R,ω>0,|θ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递减区间为( )| A. | $[\frac{5π}{12}+kπ,\frac{11π}{12}+kπ],k∈z$ | B. | $[\frac{5π}{6}+kπ≤x≤\frac{11π}{6}+kπ],k∈z$ | ||
| C. | $[\frac{5π}{12}+2kπ,\frac{11π}{12}+2kπ],k∈z$ | D. | $[-\frac{π}{12}+kπ,\frac{5π}{12}+kπ],k∈z$ |
分析 由图知f(x)在x=$\frac{5π}{12}$时取到最大值$\sqrt{2}$,且最小正周期T满足$\frac{3}{4}$T=$\frac{5π}{12}$+$\frac{π}{3}$,可求A,ω,由$\sqrt{2}sin(2×\frac{5π}{12}+θ)=\sqrt{2}$,可求$θ=-\frac{π}{3}$,解得函数解析式,令$\frac{π}{2}+2kπ≤2x-\frac{π}{3}≤\frac{3π}{2}+2kπ$即可解得f(x)的单调递减区间.
解答 解:由图知f(x)在x=$\frac{5π}{12}$时取到最大值$\sqrt{2}$,且最小正周期T满足$\frac{3}{4}$T=$\frac{5π}{12}$+$\frac{π}{3}$,
故$A=\sqrt{2}$,T=π,ω=2,
所以$\sqrt{2}sin(2×\frac{5π}{12}+θ)=\sqrt{2}$,
所以$\frac{5π}{6}+θ=\frac{π}{2}$,即$θ=-\frac{π}{3}$,
所以$f(x)=\sqrt{2}sin(2x-\frac{π}{3})$,
令$\frac{π}{2}+2kπ≤2x-\frac{π}{3}≤\frac{3π}{2}+2kπ$得$\frac{5π}{12}+kπ≤x≤\frac{11π}{12}+kπ,k∈z$.
故f(x)的单调递减区间为:$[\frac{5π}{12}+kπ,\frac{11π}{12}+kπ],k∈z$.
故选:A.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
12.下列函数中,在其定义域内既是偶函数又在(-∞,0)上单调递增的函数是( )
| A. | f(x)=x2 | B. | f(x)=2|x| | C. | f(x)=log2$\frac{1}{|x|}$ | D. | f(x)=sinx |
9.某中学安排语文、数学、英语各一名教师负责期末考试的一个考场的语文、数学、英语的监考工作,每场考试需要两名教师,则每科目的考试恰有同科目的教师监考的概率为( )
| A. | $\frac{5}{9}$ | B. | $\frac{8}{27}$ | C. | $\frac{4}{27}$ | D. | $\frac{2}{9}$ |
13.设M={2},N={2,3},则下列表示不正确的是( )
| A. | M?N | B. | M⊆N | C. | 2∈N | D. | 2?N |
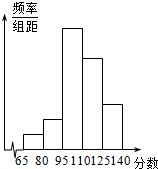 为了解某校高二学生联考数学成绩分布,从该校参加联科的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图,若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频率是6,则样本容量为40;众数为102.5.
为了解某校高二学生联考数学成绩分布,从该校参加联科的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图,若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频率是6,则样本容量为40;众数为102.5.