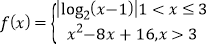题目内容
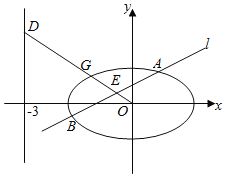
【题目】在平面直角坐标系xOy中,已知椭圆![]() ,如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于两点A,B,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
,如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于两点A,B,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
(1)求m2+k2的最小值;
(2)若|OG|2=|OD||OE|,求证:直线l过定点.
【答案】(1)2;(2)见解析
【解析】
(1)设出直线方程为![]() ,联立直线的方程和椭圆的方程,化简为一元二次方程的形式.根据直线和椭圆有两个交点得出判别式大于零,写出韦达定理,根据中点坐标公式求得
,联立直线的方程和椭圆的方程,化简为一元二次方程的形式.根据直线和椭圆有两个交点得出判别式大于零,写出韦达定理,根据中点坐标公式求得![]() 点的坐标,由此求得直线
点的坐标,由此求得直线![]() 的斜率和方程,根据
的斜率和方程,根据![]() 点坐标求得
点坐标求得![]() 的关系式,结合基本不等式求得
的关系式,结合基本不等式求得![]() 的最小值.(2)将直线
的最小值.(2)将直线![]() 的方程代入椭圆方程,求得
的方程代入椭圆方程,求得![]() 点坐标,结合
点坐标,结合![]() 两点坐标以及两点间的距离公式,求得
两点坐标以及两点间的距离公式,求得![]() ,代入
,代入![]() 列方程,解方程求得
列方程,解方程求得![]() 的关系,由此判断出直线过定点.
的关系,由此判断出直线过定点.
(1)设直线l的方程为y=kx+t(k>0),由题意,t>0,
由方程组 ,得(3k2+1)x2+6ktx+3t2﹣3=0,由题意△>0,所以3k2+1>t2,
,得(3k2+1)x2+6ktx+3t2﹣3=0,由题意△>0,所以3k2+1>t2,
设A(x1,y1),B(x2,y2),由根与系数的关系得![]() ,所以
,所以![]() ,
,
由于E为线段AB的中点,因此![]() ,
,
此时![]() ,所以OE所在直线的方程为
,所以OE所在直线的方程为![]() ,
,
又由题意知D(﹣3,m),令x=﹣3,得![]() ,即mk=1,
,即mk=1,
所以m2+k2≥2mk=2,当且仅当m=k=1时上式等号成立,
此时由△>0得0<t<2,因此当m=k=1且0<t<2时,m2+k2取最小值2.
(2)证明:由(1)知D所在直线的方程为![]() ,
,
将其代入椭圆C的方程,并由k>0,解得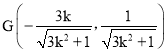 ,又
,又 ,
,
由距离公式及t>0得![]() ,
,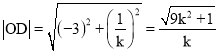 ,
,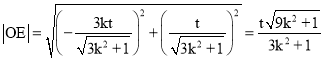 ,
,
由|OG|2=|OD||OE|,得t=k,
因此直线l的方程为y=k(x+1),所以直线l恒过定点(﹣1,0).

练习册系列答案
相关题目