Question

【题目】已知椭圆：的左、右顶点分别为，，右焦点为，且上的动点到的距离的最大值为4，最小值为2.

（1）证明：.

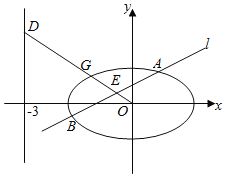
（2）若直线：与相交于，两点（，均不与，重合），且，试问是否经过定点？若经过，求出此定点坐标；若不经过，请说明理由.

Answer 1

【答案】（1）证明见解析；（2）存在，.

【解析】

（1）根据题意，可得，即可解得椭圆的标准方程，设，表示出，，利用坐标法表示，由，即可证明；

（2）联立直线与椭圆的方程，运用韦达定理可得根与系数的关系，由，运用坐标相乘可得，解出与的关系，进行判断即可得出结论.

解：（1）证明：由题意可得，解得，

则，故的方程为.

设，则.

∵，，

∴，

∵，∴.

（2）解：设，，联立，得

，

则，即，且，，

∴.

∵，，∴，

，即，

所以或.

当时，直线为，此时过定点，不合题意；

当时，直线为，此时直线过定点.