题目内容
球面上有三个点A、B、C. A和B,A和C间的球面距离等于大圆周长的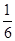 . B和C间的球面距离等于大圆周长的
. B和C间的球面距离等于大圆周长的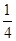 .如果球的半径是R,那么球心到截面ABC的距离等于( )
.如果球的半径是R,那么球心到截面ABC的距离等于( )
A.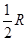 B.
B. 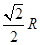 C.
C. 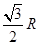 D.
D. 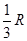
B
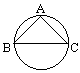
解析试题分析:如图所示,圆O是球的大圆,且大圆所在平面与面ABC垂直,其中弦EF是过A、B、C的小圆的直径,弦心距OD就是球心O到截面ABC的距离,OE是球的半径,因此,欲求OD,需先求出截面圆ABC的半径.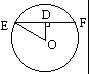
下一个图是过A、B、C的小圆.AB、AC、CB是每两点之间的直线段.它们的长度要分别在△AOB、△AOC、△COB中求得(O是球心).由于A、B间球面距离是大圆周长的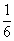 ,所以∠AOB=
,所以∠AOB=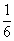 ×2π=
×2π=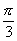 ,同理∠AOC=
,同理∠AOC=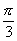 ,∠BOC=
,∠BOC=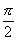 .
. 
∴|AB|=R, |AC|=R, |BC|=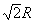 .在△ABC中,由于AB2+AC2=BC2.∴∠BAC=90°,BC是小圆ABC的直径. ∴|ED|=
.在△ABC中,由于AB2+AC2=BC2.∴∠BAC=90°,BC是小圆ABC的直径. ∴|ED|=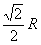 ,从而|OD|=
,从而|OD|=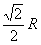 .故应选B.
.故应选B.
考点:点到平面的距离;球的有关性质。
点评:本题考查球面距离的概念及学生的空间想像能力以及对球的性质认识及利用,有关几何体的外接球,是常考知识点,也是难点,我们在平常做题时应注意总结。

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案圆C1 :(x+1)2+(y+4)2=16与圆C2 : (x-2)2+(y+2)2=9的位置关系是( ).
| A.相交 | B.外切 | C.内切 | D.相离 |
若点 在圆C:
在圆C:  的外部,则直线
的外部,则直线 与圆C的位置关系是( )
与圆C的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.相交或相切 |
已知点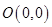 ,
,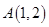 ,
,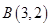 ,以线段
,以线段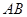 为直径作圆
为直径作圆 ,则直线
,则直线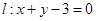 与圆
与圆 的位置关系是
的位置关系是
| A.相交且过圆心 | B.相交但不过圆心 | C.相切 | D.相离 |
直线 与圆
与圆 相交于M、N两点,若
相交于M、N两点,若 ,则k的取值范围为( )
,则k的取值范围为( )
A. | B. | C. | D.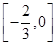 |
两圆相交于点 ,两圆的圆心均在直线
,两圆的圆心均在直线 上,则
上,则 的值为( )
的值为( )
A. | B. | C. | D. |
 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、 ,则称P优于
,则称P优于 ,如果
,如果
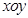 中,圆
中,圆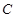 的方程为
的方程为 ,若直线
,若直线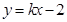 上至少存在一点,使得以该点为圆心,
上至少存在一点,使得以该点为圆心,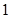 为半径的圆与圆
为半径的圆与圆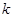 的最大值为
的最大值为 
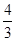


 D、8
D、8