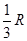题目内容
在平面直角坐标系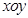 中,圆
中,圆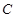 的方程为
的方程为 ,若直线
,若直线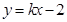 上至少存在一点,使得以该点为圆心,
上至少存在一点,使得以该点为圆心,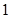 为半径的圆与圆
为半径的圆与圆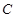 有公共点,则
有公共点,则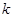 的最大值为
的最大值为
A. | B.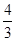 | C. | D. |
B
解析试题分析:∵圆C的方程可化为: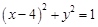 ,∴圆C的圆心为
,∴圆C的圆心为 ,半径为1。
,半径为1。
∵由题意,直线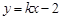 上至少存在一点
上至少存在一点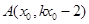 ,以该点为圆心,1为半径的圆与圆
,以该点为圆心,1为半径的圆与圆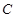 有公共点;∴存在
有公共点;∴存在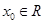 ,使得
,使得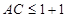 成立,即
成立,即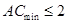 。∵
。∵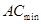 即为点
即为点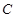 到直线
到直线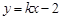 的距离
的距离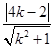 ,∴
,∴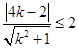 ,解得
,解得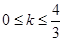 。∴
。∴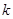 的最大值是
的最大值是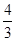 。
。
考点:本题考查了直线与圆的位置关系
点评:解题的关键是通过分析将题设条件转化为圆心到直线的距离不超过2从而建立不等式,最后确定出范围

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
当 为任意实数时,直线
为任意实数时,直线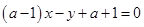 恒过定点
恒过定点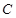 ,则以
,则以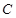 为圆心,半径为
为圆心,半径为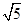 的圆是( )
的圆是( )
A.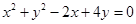 | B.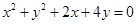 |
C.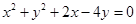 | D.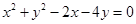 |
已知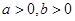 ,若直线
,若直线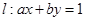 平分圆
平分圆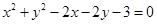 的周长,则
的周长,则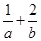 的最小值为
的最小值为
A.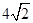 | B.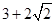 | C.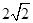 | D.1 |
直线 与圆
与圆 交于A、B两点,O是坐标原点,若直线OA、OB的倾斜面角分别为
交于A、B两点,O是坐标原点,若直线OA、OB的倾斜面角分别为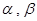 ,则
,则 ( )
( )
A. | B. | C. | D. |
若圆C的半径为1,圆心在第一象限,且与直线 和
和 轴都相切,则该圆的标准方程是( )
轴都相切,则该圆的标准方程是( )
A. | B.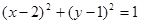 |
C. | D. |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值( )
引切线,则切线长的最小值( )
A. | B. |
C. | D. |
已知圆C: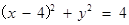 ,从动圆M:
,从动圆M: 上的动点P向圆C引切线,切点分别是E,F,则
上的动点P向圆C引切线,切点分别是E,F,则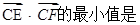 ( )
( )
A. | B. | C. | D. |
若点 为圆
为圆 的弦
的弦 的中点,则弦
的中点,则弦 所在直线方程为( )
所在直线方程为( )
A. | B. | C. | D. |
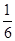 . B和C间的球面距离等于大圆周长的
. B和C间的球面距离等于大圆周长的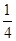 .如果球的半径是R,那么球心到截面ABC的距离等于( )
.如果球的半径是R,那么球心到截面ABC的距离等于( )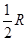 B.
B. 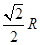 C.
C. 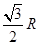 D.
D.