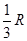题目内容
若点 在圆C:
在圆C:  的外部,则直线
的外部,则直线 与圆C的位置关系是( )
与圆C的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.相交或相切 |
C
解析试题分析:由点 在圆C:
在圆C:  的外部得
的外部得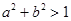 ,圆心
,圆心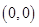 到直线
到直线 的距离
的距离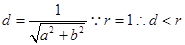 ,所以直线与圆相交
,所以直线与圆相交
考点:点与圆,直线与圆的位置关系
点评:判断点与圆的位置关系要比较点与圆心的距离与圆的半径的大小;判断直线与圆的位置关系要比较圆心到直线的距离与圆的半径的大小,若 则直线与圆相交,若
则直线与圆相交,若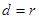 则直线与圆相切,若
则直线与圆相切,若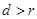 则直线与圆相离
则直线与圆相离

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知圆C1: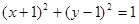 ,圆C2与圆C1关于直线
,圆C2与圆C1关于直线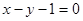 对称,则圆C2的方程为
对称,则圆C2的方程为
A.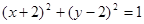 | B.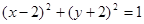 |
C.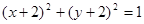 | D.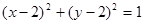 |
圆心为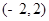 ,半径为5的圆的标准方程为( )
,半径为5的圆的标准方程为( )
A.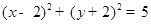 | B.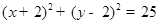 |
C.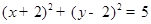 | D.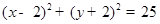 |
如果圆x2+y2+Dx+Ey+F=0与x轴切于原点, 那么( )
| A.D=0,E≠0, F≠0 | B.E=F=0,D≠0 | C.D="F=0," E≠0 | D.D=E=0,F≠0 |
已知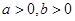 ,若直线
,若直线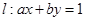 平分圆
平分圆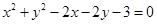 的周长,则
的周长,则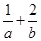 的最小值为
的最小值为
A.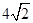 | B.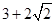 | C.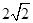 | D.1 |
以点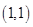 和
和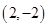 为直径两端点的圆的方程是( )
为直径两端点的圆的方程是( )
A.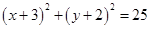 | B.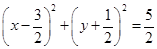 |
C.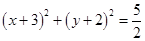 | D. |
过定点 作直线
作直线 ,使
,使 与抛物线
与抛物线 有且仅有一个公共点,这样的直线
有且仅有一个公共点,这样的直线 共有( )
共有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
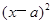 +
+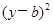 =
=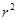 (ab≠0,r>0)的图像可能是
(ab≠0,r>0)的图像可能是
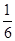 . B和C间的球面距离等于大圆周长的
. B和C间的球面距离等于大圆周长的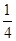 .如果球的半径是R,那么球心到截面ABC的距离等于( )
.如果球的半径是R,那么球心到截面ABC的距离等于( )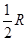 B.
B. 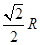 C.
C. 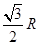 D.
D.