题目内容
直线 与圆
与圆 相交于M、N两点,若
相交于M、N两点,若 ,则k的取值范围为( )
,则k的取值范围为( )
A. | B. | C. | D.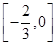 |
B
解析试题分析:由弦长公式得,圆心到直线的距离小于或等于1,即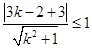 ,∴
,∴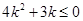 ,∴-
,∴-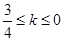 ,故选A
,故选A
考点:本题考查了圆中重要三角形的运用及不等式的解法
点评:掌握圆心到直线的距离公式及弦长公式是解决此类问题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆心为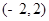 ,半径为5的圆的标准方程为( )
,半径为5的圆的标准方程为( )
A.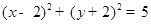 | B.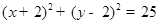 |
C.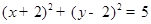 | D.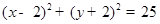 |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值( )
引切线,则切线长的最小值( )
A. | B. |
C. | D. |
若直线 与圆C:
与圆C: 相交,则点
相交,则点 的位置是( )
的位置是( )
| A.在圆C外 | B.在圆C内 | C.在圆C上 | D.以上都可能 |
已知圆C: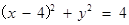 ,从动圆M:
,从动圆M: 上的动点P向圆C引切线,切点分别是E,F,则
上的动点P向圆C引切线,切点分别是E,F,则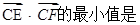 ( )
( )
A. | B. | C. | D. |
过定点 作直线
作直线 ,使
,使 与抛物线
与抛物线 有且仅有一个公共点,这样的直线
有且仅有一个公共点,这样的直线 共有( )
共有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
将圆x2+y2 -2x-4y+1=0平分的直线是
| A. x+y-1=0 | B.x+y+3=0 | C.x-y+1=0 | D.x-y+3=0 |
动点在圆x2+y2=1上移动时,它与定点B(3,0)连线的中点轨迹方程是( )
| A.(x+3)2+y2=4 | B.(x-3)2+y2=1 |
| C.(2x-3)2+4y2=1 | D.(x+ )2+y2= )2+y2= |
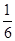 . B和C间的球面距离等于大圆周长的
. B和C间的球面距离等于大圆周长的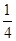 .如果球的半径是R,那么球心到截面ABC的距离等于( )
.如果球的半径是R,那么球心到截面ABC的距离等于( )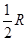 B.
B. 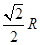 C.
C. 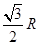 D.
D.