题目内容
12. 如图,正方体ABCD-A1B1C1D1,下列四个结论:
如图,正方体ABCD-A1B1C1D1,下列四个结论:(1)AC1⊥BD;(2)BD∥平面CB1D1;(3)AC1⊥平面CB1D1
(4)异面直线AD,CB1所成角为$\frac{π}{3}$,其中正确命题的序号有(1)(2)(3).
分析 根据线面垂直的判定定理,线面垂直的性质,线面平行的判定定理,以及异面直线所成角的概念及其求法即可判断每个命题的真假,从而得出正确答案.
解答 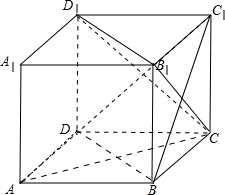 解:如图,
解:如图,
(1)连接AC,∵CC1⊥底面ABCD,BD?底面ABCD;
∴CC1⊥BD,即BD⊥CC1;
又BD⊥AC,AC∩CC1=C;
∴BD⊥平面ACC1;
∴BD⊥AC1;
∴该命题正确;
(2)∵BD∥B1D1,B1D1?平面CB1D1,BD?平面CB1D1;
∴BD∥平面CB1D1;
∴该命题正确;
(3)连接BC1,则B1C⊥BC1;
又AB⊥B1C,即B1C⊥AB,AB∩BC1=B;
∴B1C⊥平面ABC1;
∴AC1⊥B1C;
又B1D1∥BD,AC1⊥BD;
∴AC1⊥B1D1,B1D1∩B1C=B1;
∴AC1⊥平面CB1D1;
∴该命题正确;
(4)∵BC∥AD;
∴$∠{B}_{1}CB=\frac{π}{4}$为异面直线AD,CB1所成角;
∴该命题错误;
∴正确命题的序号为:(1)(2)(3).
点评 考查线面垂直的判定定理及其性质,线面平行的判定定理,以及异面直线所成角的概念及其求法.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.执行如图所示的程序框图,输出的S的值为( )


| A. | 256 | B. | 254 | C. | 258 | D. | 252 |
20.已知△ABC中,$\overrightarrow{AB}+\overrightarrow{AC}=λ(\frac{{\overrightarrow{AB}}}{{|\overrightarrow{AB}|}}+\frac{{\overrightarrow{AC}}}{{|\overrightarrow{AC}|}})$,则三角形的形状一定是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
7.某产品的广告费用支出x(万元)与产品销售额y(万元)之间的统计数据如表:
求得回归直线方程为$\widehat{y}$=bx+17.5,若投入12万元的广告费用,估计销售额为( )
| 广告费用支出x(万元) | 2 | 4 | 5 | 6 | 8 |
| 产品销售额y(万元) | 30 | 40 | 60 | 50 | 70 |
| A. | 82.5万元 | B. | 90万元 | C. | 95.5万元 | D. | 100.5万元 |
2.随机变量X的概率分布如下:
则E(X)=2.6.
| X | 1 | 2 | 3 | 4 |
| P | 0.2 | 0.3 | p | 0.3 |
 如图3,正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
如图3,正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论: