题目内容
如果f(x)=ax3+bx2+c(a>0)的导函数图象的顶点坐标为(1,- 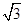 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
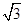 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )A.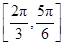 | B.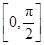 ∪ ∪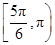 |
C.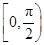 ∪ ∪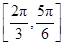 | D.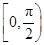 ∪ ∪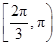 |
D
∵f′(x)=3ax2+2bx(a>0),
∴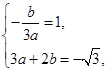 解得
解得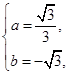
∴f′(x)=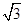 x2-2
x2-2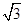 x=
x=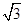 (x-1)2-
(x-1)2-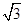 ≥-
≥-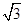 .
.
即tan α≥-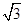 ,故切线倾斜角的范围是
,故切线倾斜角的范围是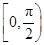 ∪
∪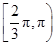 .故选D.
.故选D.
∴
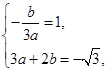 解得
解得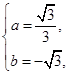
∴f′(x)=
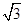 x2-2
x2-2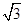 x=
x=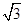 (x-1)2-
(x-1)2-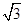 ≥-
≥-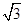 .
.即tan α≥-
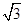 ,故切线倾斜角的范围是
,故切线倾斜角的范围是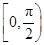 ∪
∪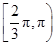 .故选D.
.故选D.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
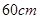 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?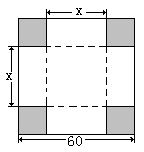
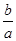 的取值范围是________.
的取值范围是________.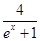 上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )
上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )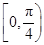
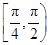
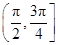
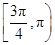
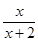 在点(-1,-1)处的切线方程为________.
在点(-1,-1)处的切线方程为________.