题目内容
设函数f(x)＝x3＋2ax2＋bx＋a，g(x)＝x2－3x＋2，其中x∈
R，a，b为常数，已知曲线y＝f(x)与y＝g(x)在点(2,0)处有相同的切线l.
求a，b的值，并求出切线l的方程．
R，a，b为常数，已知曲线y＝f(x)与y＝g(x)在点(2,0)处有相同的切线l.
求a，b的值，并求出切线l的方程．
x－y－2＝0
f′(x)＝3x2＋4ax＋b，g′(x)＝2x－3，
由于曲线y＝f(x)与y＝g(x)在点(2,0)处有相同的切线，∴f′(2)＝g′(2)，f(2)＝g(2)＝0，∴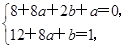
∴a＝－2，b＝5.
所以，所求切线的斜率为g′(2)＝1，
切线方程为y－0＝1(x－2)，即x－y－2＝0.
由于曲线y＝f(x)与y＝g(x)在点(2,0)处有相同的切线，∴f′(2)＝g′(2)，f(2)＝g(2)＝0，∴
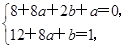∴a＝－2，b＝5.所以，所求切线的斜率为g′(2)＝1，
切线方程为y－0＝1(x－2)，即x－y－2＝0.
练习册系列答案
相关题目
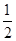x－cosx在x＝
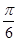处的切线方程为________．
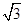),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )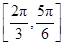
∪
∪
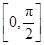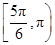
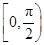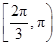
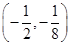
ax2－(2a＋1)x＋2ln x，a∈R.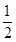
gt2，t＝2时的瞬时速度为19.6，则g＝________.