题目内容
求曲线y=x3在点(3,27)处的切线与两坐标轴所围成的三角形的面积.
54
∵f′(3)=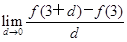 =
=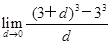 =
=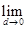 (d2+9d+27)=27,
(d2+9d+27)=27,
∴曲线在点(3,27)处的切线方程为y-27=27(x-3),即27x-y-54=0.
此切线与x轴、y轴的交点分别为(2,0),(0,-54).
∴切线与两坐标轴围成的三角形的面积为S=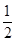 ×2×54=54.
×2×54=54.
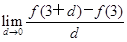 =
=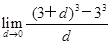 =
=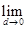 (d2+9d+27)=27,
(d2+9d+27)=27,∴曲线在点(3,27)处的切线方程为y-27=27(x-3),即27x-y-54=0.
此切线与x轴、y轴的交点分别为(2,0),(0,-54).
∴切线与两坐标轴围成的三角形的面积为S=
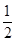 ×2×54=54.
×2×54=54.
练习册系列答案
相关题目
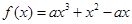 ,其中
,其中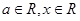 .
.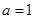 时,求函数
时,求函数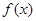 在
在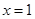 处的切线方程;
处的切线方程;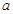 的取值范围;
的取值范围;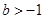 ,如果存在
,如果存在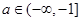 ,使得函数
,使得函数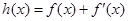
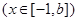 在
在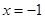 处取得最小值,试求
处取得最小值,试求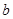 的最大值.
的最大值.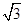 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )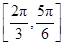
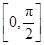 ∪
∪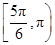
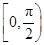 ∪
∪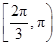
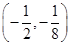
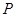 是曲线
是曲线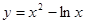 上任意一点, 则点
上任意一点, 则点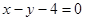 的距离的最小值是 .
的距离的最小值是 .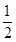 gt2,t=2时的瞬时速度为19.6,则g=________.
gt2,t=2时的瞬时速度为19.6,则g=________.