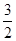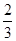题目内容
已知点P在曲线y=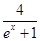
上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )
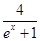上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )A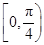． | B． |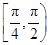
C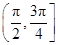． | D． |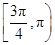
D
法一 ∵y′=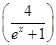
′=
=
,
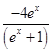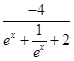由于ex+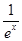
≥2当且仅当ex=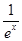即x=0时等号成立,
∴-1≤y′<0,即-1≤tanα<0,
由正切函数图象得α∈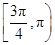.故选D.
法二 由于y′=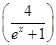′=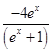<0,倾斜角必为钝角,故排除选项A和B.
又因为y′|x=1=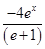
=-
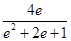>-1,因此倾斜角必然大于
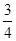π,由此排除选项C.故选D.
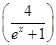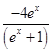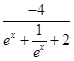′==,由于ex+
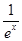≥2当且仅当ex=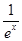即x=0时等号成立,∴-1≤y′<0,即-1≤tanα<0,
由正切函数图象得α∈
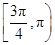.故选D.法二 由于y′=
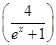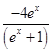′=<0,倾斜角必为钝角,故排除选项A和B.又因为y′|x=1=
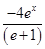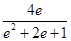=->-1,因此倾斜角必然大于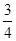π,由此排除选项C.故选D.
练习册系列答案
科学实验活动册系列答案
相关题目
，
，
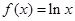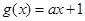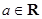，记
.
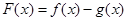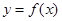在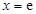
处的切线方程；
的单调区间；
时，若函数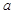
的取值范围.
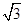),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )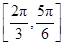
∪
∪
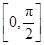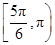
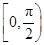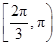
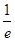
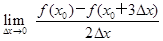＝1，则f′(x0)等于( )．
