题目内容
7.若m∈R,命题p:设x1,x2是方程x2-ax-3=0的两个实根,不等式|m+1|≥|x1-x2|对任意实数a∈[-2,2]恒成立,命题q:函数f(x)=x3+mx2+(m+$\frac{10}{3}$)x+3在(-∞,+∞)上有极值,求使p且¬q为真命题,求实数m的取值范围.分析 对于p,先求出|x1-x2|∈[2$\sqrt{3}$,4],再根据不等式|m+1|≥|x1-x2|对任意实数a∈[-2,2]恒成立,得到|m+1|≥4,解得m的范围,
对于q,函数f(x)=x3+mx2+(m+$\frac{10}{3}$)x+3在(-∞,+∞)上有极值,则f′(x)=3x2+2mx+(m+$\frac{10}{3}$)=0有实根,根据判别式求出a的范围,
由于p且¬q为真命题,得到p真,q假,问题得解.
解答 解:若命题p为真命题,
∵x1,x2是方程x2-ax-3=0的两个实根
∴x1+x2=a,x1x2=-3,
∴|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{{a}^{2}+12}$,
∵a∈[-2,2],
∴|x1-x2|∈[2$\sqrt{3}$,4],
∵|m+1|≥|x1-x2|对任意实数a∈[-2,2]恒成立,
则只要|m+1|≥|x1-x2|max在a∈[-2,2]成立即可
∴|m+1|≥4
∴m+1≥4或m+1≤-4,
∴m≥3,或m≤-5,
若命题q为真命题,
∵f(x)=x3+mx2+(m+$\frac{10}{3}$)x+3,
∴f′(x)=3x2+2mx+(m+$\frac{10}{3}$),
∵函数f(x)=x3+mx2+(m+$\frac{10}{3}$)x+3在(-∞,+∞)上有极值,
∴f′(x)=3x2+2mx+(m+$\frac{10}{3}$)=0有实根,
∴△=4m2-12m-40≥0,
解得m≤-2,或m≥5,
∵p且¬q为真命题,
∴p真,q假,
∴$\left\{\begin{array}{l}{m≥3,或m≤-5}\\{-2<m<5}\end{array}\right.$,
解得3≤m<5,
实数m的取值范围为[3,5)
点评 本题目主要考查了复合命题的真假判断的应用,解题得关键是熟练应用函数的知识准确求出命题P,Q为真时的m的取值范围,属于中档题.

| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 不能确定 |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
| A. | $\frac{12+3\sqrt{3}}{26}$ | B. | $\frac{12+5\sqrt{3}}{26}$ | C. | $\frac{6+3\sqrt{3}}{13}$ | D. | $\frac{6+4\sqrt{3}}{13}$ |
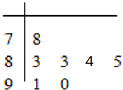 在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85和6.8 | B. | 85和1.6 | C. | 86和6.8 | D. | 86和1.6 |