题目内容
2．（1）求y=x+$\frac{1}{x-2}$（x＞2）得最小值．（2）求（x+y）（$\frac{1}{x}$+$\frac{1}{y}$）的最小值，其中x＞0，y＞0．
分析 （1）变形为（x-2）$+\frac{1}{x-2}$$≥2\sqrt{（x-2）\frac{1}{x-2}}$=2（x=3时等号成立）即可求解．
（2）展开（x+y）（$\frac{1}{x}$+$\frac{1}{y}$）=2$+\frac{x}{y}$$+\frac{y}{x}$，其中x＞0，y＞0，利用不等式求解即可．
解答 解：（1）∵x＞2，x-2＞0，
∴（x-2）$+\frac{1}{x-2}$$≥2\sqrt{（x-2）\frac{1}{x-2}}$=2（x=3时等号成立）
∴x+$\frac{1}{x-2}$的最小值为2+2=4
故y的最小值为4，当且仅当x=3时等号成立
（2）$\frac{x}{y}$$+\frac{y}{x}$$≥2\sqrt{\frac{x}{y}\frac{y}{x}}$=2，
∴2$+\frac{x}{y}$$+\frac{y}{x}$≥4（x=y时等号成立）
故最小值为4，当且仅当x=y时等号成立
点评 本题考察了基本不等式的运用求解函数的最值，关键是恒等变形，确定等号成立的条件，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
13．如图，在等腰△ABC中，AB=AC=1，∠A=120°，则向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$上的投影等于（ ）
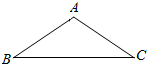
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
10．设实数x，y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y≤2\end{array}$，则u=$\frac{x+y}{x}$的取值范围是（ ）
| A． | $[{\frac{4}{3}，\frac{3}{2}}]$ | B． | $[{\frac{1}{3}，2}]$ | C． | $[{\frac{4}{3}，3}]$ | D． | $[{\frac{3}{2}，3}]$ |
17．
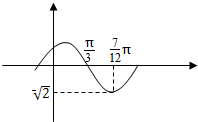函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，
（1）求函数f（x）的解析式；
（2）解不等式f（x）≤1．
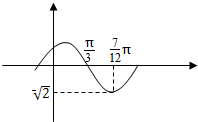函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，（1）求函数f（x）的解析式；
（2）解不等式f（x）≤1．
11．已知定义在R上的奇函数f（x），满足f（x+4）=f（x），则f（8）的值为（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |