题目内容
18.已知函数y=lg(mx2+2x+m-1).(1)若函数的定义域为R,求实数m的取值范围;
(2)若函数的定义域为M,且(0,3)⊆M,求m的取值范围.
分析 (1)由题意可得mx2+2x+m-1>0恒成立,对m讨论,m=0和m>0,判别式△<0,解不等式即可得到所求范围;
(2)由题意可得mx2+2x+m-1>0在(0,3)上恒成立,运用参数分离和导数,求得右边函数的最值,再由恒成立思想即可得到所求范围.
解答 解:(1)若函数的定义域为R,
则mx2+2x+m-1>0恒成立,
当m=0时,2x-1>0不恒成立,故舍去;
当m>0,且判别式△=4-4m(m-1)<0,
解得m>$\frac{1+\sqrt{5}}{2}$或m<$\frac{1-\sqrt{5}}{2}$,
则有m>$\frac{1+\sqrt{5}}{2}$;
即有m的取值范围是($\frac{1+\sqrt{5}}{2}$,+∞);
(2)由题意可得mx2+2x+m-1>0在(0,3)上恒成立,
即为m>$\frac{1-2x}{1+{x}^{2}}$在(0,3)上恒成立,
令g(x)=$\frac{1-2x}{1+{x}^{2}}$,g′(x)=$\frac{2({x}^{2}-x-1)}{(1+{x}^{2})^{2}}$,
可得当0<x<$\frac{1+\sqrt{5}}{2}$时,g′(x)<0,g(x)递减,
当$\frac{1+\sqrt{5}}{2}$<x<3时,g′(x)>0,g(x)递增,
当x=$\frac{1+\sqrt{5}}{2}$处取得极小值,也为最小值,
当x=0时,g(0)=1,当x=3时,g(3)=-$\frac{1}{2}$,
由恒成立思想可得,m≥1.
即有m的取值范围为[1,+∞).
点评 本题考查对数函数的性质和运用,主要考查二次不等式恒成立问题,注意运用二次函数的图象和性质,以及导数求单调区间和最值,属于中档题.

练习册系列答案
相关题目
9.下列命题中,不正确的是( )
| A. | $|\overrightarrow a|=\sqrt{{{(\overrightarrow a)}^2}}$ | B. | λ($\overrightarrow a$•$\overrightarrow b$)=$\overrightarrow a$•(λ$\overrightarrow b$) | C. | ($\overrightarrow a$-$\overrightarrow b$)$\overrightarrow c$=$\overrightarrow a$•$\overrightarrow c$-$\overrightarrow b$•$\overrightarrow c$ | D. | $\overrightarrow a$与$\overrightarrow b$共线?$\overrightarrow a$•$\overrightarrow b$=$|{\overrightarrow a}||{\overrightarrow b}|$ |
13.如图,在等腰△ABC中,AB=AC=1,∠A=120°,则向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$上的投影等于( )
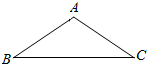

| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
10.设实数x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y≤2\end{array}$,则u=$\frac{x+y}{x}$的取值范围是( )
| A. | $[{\frac{4}{3},\frac{3}{2}}]$ | B. | $[{\frac{1}{3},2}]$ | C. | $[{\frac{4}{3},3}]$ | D. | $[{\frac{3}{2},3}]$ |
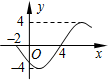 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).