题目内容
13.已知偶函数f(x)=$\left\{\begin{array}{l}{{3}^{x}+a\\;x≥0}\\{g(x)\\;x<0}\end{array}\right.$,则满足f(x-1)<f(2)的实数x的取值范围是( )| A. | (-∞,3) | B. | (3,+∞) | C. | (-1,3) | D. | (-∞,-1)∪(3,+∞) |
分析 根据指数函数的图象和性质,分析偶函数f(x)的单调性,结合f(x-1)<f(2),可得|x-1|<2,解得答案.
解答 解:当x≥0时,f(x)=3x+a为增函数,
又由函数f(x)为偶函数,
故当x<0时,f(x)为减函数,
若f(x-1)<f(2),
则|x-1|<2,
解得:x∈(-1,3),
故选:C
点评 本题考查的知识点是分段函数的应用,指数函数的单调性,偶函数的性质,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
18.在△ABC中,内角A,B,C的对边分别为a,b,c,且a=2bsinA,则B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{6}$或$\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
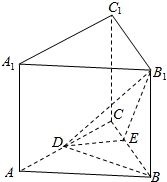 在正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点D是AC的中点,点E在棱BC上(不含端点),且DE⊥B1E.
在正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点D是AC的中点,点E在棱BC上(不含端点),且DE⊥B1E.