题目内容
【题目】过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为![]() 的直线与抛物线相交于A,B两点.
的直线与抛物线相交于A,B两点.
(1)用p表示线段AB的长;
(2)若![]() ,求这个抛物线的方程.
,求这个抛物线的方程.

【答案】(1)4p(2)y2=4x.
【解析】试题分析:(1)先根据点斜式写出直线方程,再与抛物线联立方程组,利用韦达定理得两根之和,最后根据抛物线定义求线段AB的长;(2)先根据向量数量积化简![]() ,再根据点斜式设直线方程,与抛物线联立方程组,利用韦达定理代入关系式,解出p
,再根据点斜式设直线方程,与抛物线联立方程组,利用韦达定理代入关系式,解出p
试题解析:解:(1)抛物线的焦点为F![]() ,过点F且倾斜角为
,过点F且倾斜角为![]() 的直线方程是y=x-
的直线方程是y=x-![]() .设A(x1,y1),B(x2,y2),联立
.设A(x1,y1),B(x2,y2),联立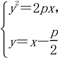
得x2-3px+![]() =0,∴x1+x2=3p,x1x2=
=0,∴x1+x2=3p,x1x2=![]() ,∴AB=x1+x2+p=4p.
,∴AB=x1+x2+p=4p.
(2)由(1)知x1x2=![]() ,x1+x2=3p,
,x1+x2=3p,
∴y1y2=![]()
![]() =x1x2-
=x1x2-![]() (x1+x2)+
(x1+x2)+![]() =
=![]() -
-![]() +
+![]() =-p2,
=-p2,
∴OA―→·OB―→=x1x2+y1y2=![]() -p2=-
-p2=-![]() =-3,
=-3,
解得p2=4,
∴p=2.
∴这个抛物线的方程为y2=4x.

练习册系列答案
相关题目