题目内容

6．已知集合A={x|x2+2x-3＜0}，B={x|-$\sqrt{2}$＜x＜1}，则A∩B等于（　　）
A．ΦB．{x|-3＜x＜1}C．{x|-$\sqrt{2}$＜x＜1}D．{x|x2+2x-3＜0}

分析 通过化简A，利用交集的定义计算即可．

解答 解：∵x2+2x-3=（x-1）（x+3）＜0，
∴-3＜x＜1，
又∵B={x|-$\sqrt{2}$＜x＜1}，
∴A∩B={x|-$\sqrt{2}$＜x＜1}，
故选：C．

点评 本题考查集合的交集运算，注意解题方法的积累，属于基础题．

练习册系列答案
相关题目
16．执行如图中的程序，如果输出的结果是-4，那么输入的x只可能是（　　）
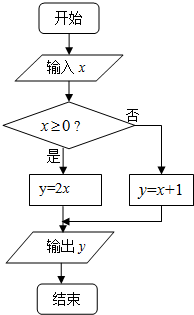
A．3B．0C．-4D．-5
17．设min{p，q}表示p，q中较小的一个，给出下列命题：
①min{x2，x-1}=x-1；
②设$θ∈（0{，_{\;}}\frac{π}{2}]$，则min$\{\frac{sinθ}{{{{sin}^2}θ+1}}{，_{\;}}\frac{1}{2}\}=\frac{1}{2}$；
③设a，b∈N*，则min$\{a{，_{\;}}\frac{2b}{{{a^2}+{b^2}}}\}$的最大值是1，
其中所有正确命题的序号有（　　）
A．①B．③C．①②D．①③
14．设min{p，q}表示p，q两者中的较小者，若函数f（x）=min{3-x，log2x}，则满足f（x）≤$\frac{1}{2}$的x的集合为（　　）
A．（0，2]∪[$\frac{5}{2}$，+∞）B．[$\sqrt{2}$，$\frac{5}{2}$]C．（0，$\sqrt{2}$]∪[$\frac{5}{2}$，+∞）D．（0，$\sqrt{2}$）∪（$\frac{5}{2}$，+∞）
1．已知函数f（x）=ex，x∈R．
（Ⅰ） 证明：曲线y=f（x）与曲线y=x+1有唯一公共点；
（Ⅱ）（i）求g（x）=x+2+（x-2）•f（x）在[0，+∞）的最小值；
（ii）若实数a，b不相等，试比较$\frac{f（a）+f（b）}{2}$与$\frac{f（b）-f（a）}{b-a}$的大小，并说明理由．
11．已知各项均为正数的数列{an}的前n项和为Sn，对任意n∈N•，都有1，$\sqrt{{S}_{n}}$，an成等差数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足bn+1+（-1）nbn=an（n∈N•），求数列{bn}的前60项和．
18．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，为得到g（x）=cosωx的图象，则只要将f（x）的图象（　　）
A．向右平移$\frac{π}{6}$个单位长度B．向左平移$\frac{π}{12}$个单位长度
C．向左平移$\frac{π}{6}$个单位长度D．向右平移$\frac{π}{12}$个单位长度
15．将函数y=sin（$2x-\frac{π}{3}）$的图象向左平移φ（φ＞0）个单位后，所得到的图象对应的函数为奇函数，则φ的最小值为（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$
16．在《爸爸去哪儿》第二季第四期中，假如村长给6位“萌娃”布置一项到A、B、C三个位置搜寻空投食物的任务，每两位“萌娃”搜寻一个位置．考虑到位置远近及年龄大小，Grace不去较远的A位置，多多不去较近的C位置，则不同的搜寻安排方案有（　　）
A．20 种B．40 种C．42种D．48种

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网