题目内容
20.设D为△ABC所在平面内一点,$\overrightarrow{AD}=2\overrightarrow{CD}$,则( )| A. | $\overrightarrow{BD}=-\overrightarrow{BA}+2\overrightarrow{BC}$ | B. | $\overrightarrow{BD}=2\overrightarrow{BA}-\overrightarrow{BC}$ | C. | $\overrightarrow{BD}=\overrightarrow{BA}+2\overrightarrow{BC}$ | D. | $\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BA}+\frac{2}{3}\overrightarrow{BC}$ |
分析 由已知条件用出图形,过A作BD平行线,交BC延长线于E,由此利用向量加法的三角形法则能求出结果.
解答 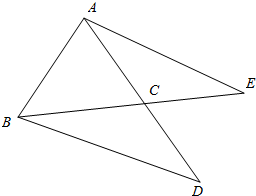 解:如图,D为△ABC所在平面内一点,$\overrightarrow{AD}=2\overrightarrow{CD}$,
解:如图,D为△ABC所在平面内一点,$\overrightarrow{AD}=2\overrightarrow{CD}$,
过A作BD平行线,交BC延长线于E,
则$\overrightarrow{BD}$=$\overrightarrow{AE}$=$\overrightarrow{AB}+2\overrightarrow{BC}$=$-\overrightarrow{BA}+2\overrightarrow{BC}$.
故选:A.
点评 本题考查向量的加法法则的应用,是基础题,解题时要认真审题,注意向量加法的三角形法则的合理运用.

练习册系列答案
相关题目
10.平面内,点P在以O为顶点的直角内部,A,B分别为两直角边上两点,已知$|{\overrightarrow{OP}}|=2$,$\overrightarrow{OP}•\overrightarrow{OA}=2$,$\overrightarrow{OP}•\overrightarrow{OB}=1$,则当|AB|最小时,sin∠AOP=( )
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
8.已知$\frac{a+i}{b+2i}$=i(a,b∈R),其中i为虚数单位,则a+b=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
12.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
| A. | y=x3 | B. | $y=|{log_2^{\;}x}|$ | C. | y=2|x| | D. | y=-x2+1 |
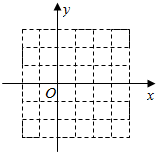 设实数x,y满足$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-4≥0\\ 2y-3≤0\end{array}\right.$(注:图中的正方形网格的边长为1个单位长度).
设实数x,y满足$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-4≥0\\ 2y-3≤0\end{array}\right.$(注:图中的正方形网格的边长为1个单位长度).