题目内容
11. 设实数x,y满足$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-4≥0\\ 2y-3≤0\end{array}\right.$(注:图中的正方形网格的边长为1个单位长度).
设实数x,y满足$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-4≥0\\ 2y-3≤0\end{array}\right.$(注:图中的正方形网格的边长为1个单位长度).(1)在给出的直角坐标系中画出平面区域;
(2)求x+3y的最大值;
(3)求$\frac{y}{x}$的范围.
分析 (1)根据二元一次不等式组的应用进行作图即可.
(2)利用平移进行求解即可.
(3)利用直线斜率的几何意义进行求解.
解答 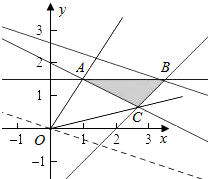 解:(1)画出如图所示的平面区域:
解:(1)画出如图所示的平面区域:
(2)由z=x+3y,得$y=-\frac{1}{3}x+\frac{z}{3}$,作出不等式对应的可行域,
平移直线$y=-\frac{1}{3}x+\frac{z}{3}$,由平移可知当直线$y=-\frac{1}{3}x+\frac{z}{3}$,经过点B(0,3)时,
直线$y=-\frac{1}{3}x+\frac{z}{3}$,的截距最大,此时z取得最大值,
由$\left\{\begin{array}{l}{2y=3}\\{x-y-2=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,即C($\frac{7}{2},\frac{3}{2}$),
代入z=x+3y,得z=$\frac{7}{2}$+$\frac{3}{2}$×3=8,
即目标函数z=x+3y的最大值为8.
(3)设k=$\frac{y}{x}$,则k的几何意义切区域内的点到原点斜率,
由图象知OA的斜率最大,OC的斜率最小,
由$\left\{\begin{array}{l}{2y-3=0}\\{x+2y-4=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=\frac{3}{2}}\end{array}\right.$,即A($\frac{3}{2}$,1),
由$\left\{\begin{array}{l}{x+2y-4=0}\\{x-y-2=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=\frac{2}{3}}\end{array}\right.$,即C($\frac{8}{3}$,$\frac{2}{3}$)
依据平面区域得${({\frac{y}{x}})_{min}}=\frac{{\frac{2}{3}}}{{\frac{8}{3}}}=\frac{1}{4},{({\frac{y}{x}})_{max}}=\frac{{\frac{3}{2}}}{1}=\frac{3}{2}$
所以$\frac{y}{x}$的范围是[$\frac{1}{4},\frac{3}{2}$].
点评 本题主要考查线性规划的应用,利用图象平移和直线斜率,求得目标函数的最大值和最小值,利用数形结合是解决线性规划问题中的基本方法.

| A. | 3 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | -sin2x | B. | -2cosx | C. | 2sinx | D. | 2cosx |
| A. | ?x0∈R,x02-3x0+5≤0 | B. | ?x0∈R,x02-3x0+5>0 | ||
| C. | ?x∈R,x2-3x+5≤0 | D. | ?x0∈R,x02-3x0+5>0 |
| A. | $\overrightarrow{BD}=-\overrightarrow{BA}+2\overrightarrow{BC}$ | B. | $\overrightarrow{BD}=2\overrightarrow{BA}-\overrightarrow{BC}$ | C. | $\overrightarrow{BD}=\overrightarrow{BA}+2\overrightarrow{BC}$ | D. | $\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BA}+\frac{2}{3}\overrightarrow{BC}$ |
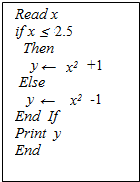 若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.
若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.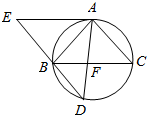 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$.