题目内容
(本小题满分12分)
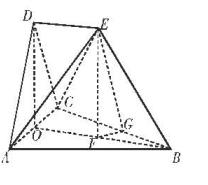
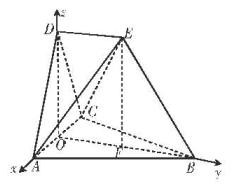
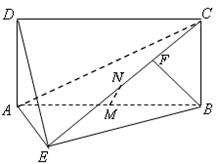
在如图所示的空间几何体中,平面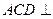 平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在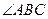 的平分线上。
的平分线上。
(1)求证:DE//平面ABC;
(2)求二面角E—BC—A的余弦;
(3)求多面体ABCDE的体积。
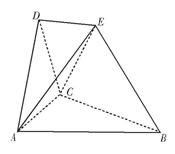
在如图所示的空间几何体中,平面
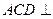 平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在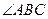 的平分线上。
的平分线上。(1)求证:DE//平面ABC;
(2)求二面角E—BC—A的余弦;
(3)求多面体ABCDE的体积。

(1)略
(2)二面角E—BC—A的余弦值为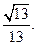
(3)多面体DE—ABC的体积为V=V1-V2=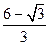
(2)二面角E—BC—A的余弦值为
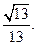
(3)多面体DE—ABC的体积为V=V1-V2=
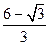
解:方法一:(1)由题意知,  都是边长为2的等边三角形,取AC中点O,连接BO,DO,则
都是边长为2的等边三角形,取AC中点O,连接BO,DO,则
 平面ACD
平面ACD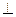 平面ABC
平面ABC
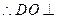 平面ABC,作EF
平面ABC,作EF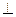 平面ABC,
平面ABC,
那么EF//DO,根据题意,点F落在BO上,
 ,易求得
,易求得
所以四边形DEFO是平行四边形,DE//OF;
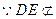 平面ABC,
平面ABC,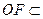 平面ABC,
平面ABC,
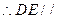 平面ABC…………4分
平面ABC…………4分
(2)作FG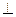 BC,垂足为G,连接FG;
BC,垂足为G,连接FG;
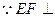 平面ABC,根据三垂线定理可知,EG
平面ABC,根据三垂线定理可知,EG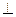 BC
BC
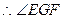 就是二面角E—BC—A的平面角
就是二面角E—BC—A的平面角
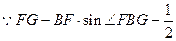
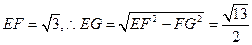
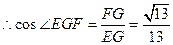
即二面角E—BC—A的余弦值为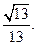 …………8分
…………8分
(3) 平面ACD
平面ACD 平面ABC,OB
平面ABC,OB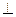 AC
AC
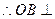 平面ACD;又
平面ACD;又
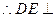 平面DAC,
平面DAC,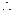 三棱锥E—DAC的体积
三棱锥E—DAC的体积
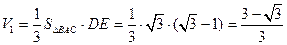
又三棱锥E—ABC的体积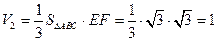
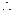 多面体DE—ABC的体积为V=V1-V2=
多面体DE—ABC的体积为V=V1-V2=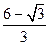 …………12分
…………12分
方法二:(1)同方法一
(2)建立如图所示的空间直角坐标系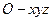 ,可求得平面ABC的一个法向量为
,可求得平面ABC的一个法向量为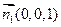 ,
,
平面BCE的一个法向量为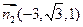 ,所以
,所以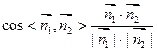
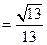
又由图知,所求二面角的平面角是锐角,所以二面角E—BC—A的余弦值为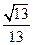
(3)同方法一
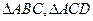 都是边长为2的等边三角形,取AC中点O,连接BO,DO,则
都是边长为2的等边三角形,取AC中点O,连接BO,DO,则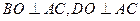

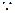 平面ACD
平面ACD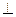 平面ABC
平面ABC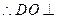 平面ABC,作EF
平面ABC,作EF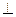 平面ABC,
平面ABC,那么EF//DO,根据题意,点F落在BO上,
 ,易求得
,易求得
所以四边形DEFO是平行四边形,DE//OF;
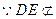 平面ABC,
平面ABC,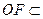 平面ABC,
平面ABC,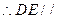 平面ABC…………4分
平面ABC…………4分(2)作FG
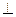 BC,垂足为G,连接FG;
BC,垂足为G,连接FG;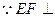 平面ABC,根据三垂线定理可知,EG
平面ABC,根据三垂线定理可知,EG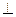 BC
BC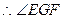 就是二面角E—BC—A的平面角
就是二面角E—BC—A的平面角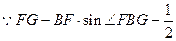
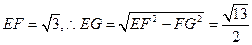
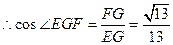
即二面角E—BC—A的余弦值为
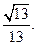 …………8分
…………8分(3)
 平面ACD
平面ACD 平面ABC,OB
平面ABC,OB AC
AC 平面ACD;又
平面ACD;又
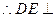 平面DAC,
平面DAC,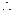 三棱锥E—DAC的体积
三棱锥E—DAC的体积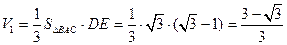
又三棱锥E—ABC的体积
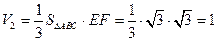
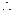 多面体DE—ABC的体积为V=V1-V2=
多面体DE—ABC的体积为V=V1-V2=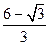 …………12分
…………12分方法二:(1)同方法一
(2)建立如图所示的空间直角坐标系
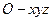 ,可求得平面ABC的一个法向量为
,可求得平面ABC的一个法向量为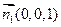 ,
,平面BCE的一个法向量为
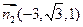 ,所以
,所以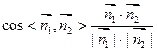
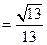
又由图知,所求二面角的平面角是锐角,所以二面角E—BC—A的余弦值为
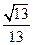

(3)同方法一

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目

 的正方体
的正方体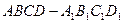 中,
中,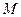 是
是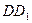 的中点,
的中点,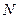 在线段
在线段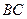 上,且
上,且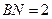 .
.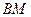 与
与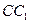 所成角的余弦值;
所成角的余弦值;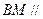 面
面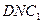 ;
;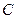 到面
到面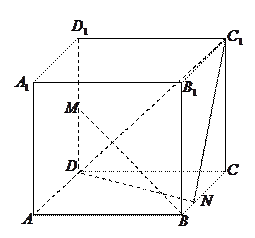
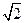 .
.
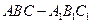 所有棱
所有棱 长都是
长都是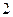 ,
,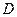 是棱
是棱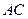 的中点,
的中点,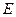 是棱
是棱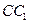 的中点,
的中点,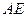 交
交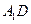 于点
于点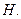
 ;
;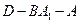 的大小(用反三角函数表示);
的大小(用反三角函数表示);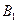 到平面
到平面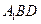 的距离.
的距离.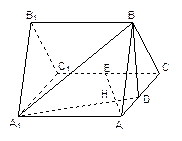
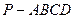 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱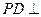 底面ABCD,
底面ABCD,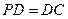 ,E是PC的中点.
,E是PC的中点.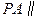 平面
平面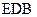 ;
;
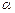 、
、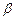 为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )
为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )
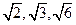 ,则对角线长为( )
,则对角线长为( )