题目内容
【题目】综合题。
（1）已知 
在区间（m2﹣4m，2m﹣2）上能取得最大值，求实数m的取值范围；
（2）设函数f（x）=ax﹣（k﹣1）a﹣x（a＞0且a≠1）是定义域为R的奇函数，若 
，且g（x）=a2x+a﹣2x﹣2mf（x）在[1，+∞）上的最小值为﹣2，求m的值．
【答案】
（1）解：作函数 
的图象如下，
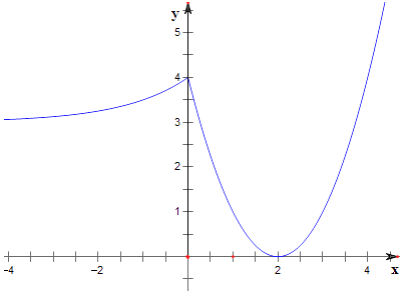
结合图象可知， ；解得1＜m≤3；
故实数m的取值范围为（1，3]
（2）解：由题意，对任意x∈R，f（﹣x）=﹣f（x）
即a﹣x﹣（k﹣1）ax=﹣ax+（k﹣1）a﹣x，
即（k﹣1）（ax+a﹣x）﹣（ax+a﹣x）=0，（k﹣2）（ax+a﹣x）=0，
因为x为任意实数，所以k=2．
∵f（x）=ax﹣a﹣x，∴ 
，∴ 
，解得a=2．
故f（x）=2x﹣2﹣x，g（x）=22x+2﹣2x﹣2m（2x﹣2﹣x），
令t=2x﹣2﹣x，易得t为增函数，由x∈[1，+∞），得 
，
则22x+2﹣2x=t2+2，∴ 
．
当 
时，h（t）在 
上是增函数，则 
，
解得 
（舍去）．当 
时，h（m）2﹣m2=﹣2，解得m=2，或m=﹣2（舍去）．
综上，m的值是2
【解析】（1）作函数 
的图象，在区间（m2﹣4m，2m﹣2）上能取得最大值，可得， ，即可求实数m的取值范围；（2）求出f（x）=2x﹣2﹣x ， g（x）=22x+2﹣2x﹣2m（2x﹣2﹣x），再根据g（x）=a2x+a﹣2x﹣2mf（x）在[1，+∞）上的最小值为﹣2，即可求m的值．
【考点精析】通过灵活运用函数的最值及其几何意义和函数奇偶性的性质，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值；在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇即可以解答此题．
