题目内容
【题目】若f（x）=x2﹣x+b，且f（log2a）=b，log2[f（a）]=2（a≠1）．
（1）求f（log2x）的最小值及对应的x值；
（2）x取何值时，f（log2x）＞f（1）且log2[f（x）]＜f（1）？
【答案】
（1）解：∵f（x）=x2﹣x+b，∴f（log2a）=log22a﹣log2a+b．
由已知有log22a﹣log2a+b=b，∴（log2a﹣1）log2a=0．
∵a≠1，∴log2a=1．∴a=2．
又log2[f（a）]=2，∴f（a）=4．
∴a2﹣a+b=4，b=4﹣a2+a=2．
故f（x）=x2﹣x+2，从而f（log2x）=log22x﹣log2x+2=（log2x﹣ 
）2+ 
．
∴当log2x= 即x= 
时，f（log2x）有最小值
（2）解：由题意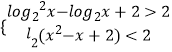 
0＜x＜1
【解析】（1）把log2a代入f（x）中，解关于log2a的一元二次方程，求出a的值；再把f（a）的值代入log2[f（a）]=2中，求出b的值；从而确定函数f（x）的解析式；把log2x代入函数f（x）中，配方法求f（log2x）的最小值及对应的x值；（2）利用对数恒等式和对数函数的单调性解不等式．
练习册系列答案
相关题目
