题目内容
【题目】已知圆![]() :
: ![]() 过椭圆
过椭圆![]() :
: ![]() (
(![]() )的短轴端点,
)的短轴端点, ![]() ,
, ![]() 分别是圆
分别是圆![]() 与椭圆
与椭圆![]() 上任意两点,且线段
上任意两点,且线段![]() 长度的最大值为3.
长度的最大值为3.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作圆
作圆![]() 的一条切线交椭圆
的一条切线交椭圆![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的面积的最大值.
的面积的最大值.
【答案】(Ⅰ)![]() (Ⅱ)1.
(Ⅱ)1.
【解析】试题分析: (Ⅰ)根据椭圆几何性质得线段![]() 长度的最大值为
长度的最大值为![]() ,且
,且![]() ,解出
,解出![]() ,得椭圆
,得椭圆![]() 的方程;(Ⅱ)利用点斜式设直线方程,与椭圆方程联立,结合韦达定理及弦长公式可得底边
的方程;(Ⅱ)利用点斜式设直线方程,与椭圆方程联立,结合韦达定理及弦长公式可得底边![]() 长(用斜率及
长(用斜率及![]() 表示);利用点到直线距离公式得三角形的高(用斜率及
表示);利用点到直线距离公式得三角形的高(用斜率及![]() 表示);根据圆心到切线距离等于半径得斜率与
表示);根据圆心到切线距离等于半径得斜率与![]() 关系,代入面积公式并化简得关于
关系,代入面积公式并化简得关于![]() 的函数关系式,最后利用基本不等式求最值.
的函数关系式,最后利用基本不等式求最值.
试题解析:解:(Ⅰ)∵圆![]() 过椭圆
过椭圆![]() 的短轴端点,∴
的短轴端点,∴![]() ,又∵线段
,又∵线段![]() 长度的最大值为3,
长度的最大值为3,
∴![]() ,即
,即![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)由题意可设切线![]() 的方程为
的方程为![]() ,即
,即![]() ,则
,则![]() ,得
,得![]() .①
.①
联立得方程组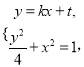 消去
消去![]() 整理得
整理得![]() .
.
其中![]() ,
,
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
则![]() .②
.②
将①代入②得![]() ,∴
,∴![]() ,
,
而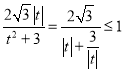 ,等号成立当且仅当
,等号成立当且仅当![]() ,即
,即![]() .
.
综上可知: ![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目