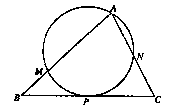题目内容
选修4-1几何证明选讲,如图,D,E分别是AB,AC边上的点,且不与顶点重合,已知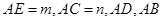 为方程
为方程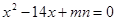 的两根,
的两根,
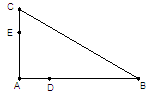
(1) 证明 C,B,D,E四点共圆;
(2)若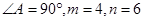 ,求C,B,D,E四点所在圆的半径。
,求C,B,D,E四点所在圆的半径。
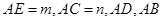 为方程
为方程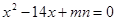 的两根,
的两根,
(1) 证明 C,B,D,E四点共圆;
(2)若
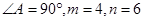 ,求C,B,D,E四点所在圆的半径。
,求C,B,D,E四点所在圆的半径。(1)见解析(2)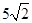
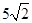
本试题主要是考查了四点共圆的证明以及圆的半径的求解综合运用。
(1)由于连接DE,根据题意在△ADE和△ACB中,结合根与系数的关系可知△ADE∽△ACB,那么因此 ∠ADE=∠ACB , 所以C,B,D,E四点共圆。
(2)m="4," n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
结合平行关系得到结论。
解:(I)连接DE,根据题意在△ADE和△ACB中,
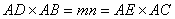
即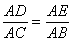 .又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。
.又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。
(Ⅱ)m="4," n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=900,故GH∥AB, HF∥AC. HF=AG=5,DF= (12-2)=5.
(12-2)=5.
故C,B,D,E四点所在圆的半径为5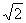
(1)由于连接DE,根据题意在△ADE和△ACB中,结合根与系数的关系可知△ADE∽△ACB,那么因此 ∠ADE=∠ACB , 所以C,B,D,E四点共圆。
(2)m="4," n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
结合平行关系得到结论。
解:(I)连接DE,根据题意在△ADE和△ACB中,
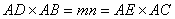
即
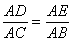 .又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。
.又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。(Ⅱ)m="4," n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=900,故GH∥AB, HF∥AC. HF=AG=5,DF=
 (12-2)=5.
(12-2)=5.故C,B,D,E四点所在圆的半径为5

练习册系列答案
相关题目
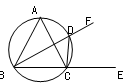
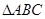 的角平分线AD的延长线交它的外接圆于点E
的角平分线AD的延长线交它的外接圆于点E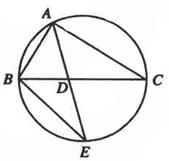
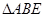
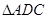
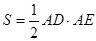 ,求
,求 的大小。
的大小。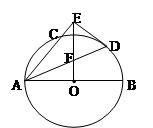
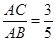 ,求
,求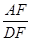 的值.
的值.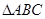 中,
中,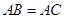 ,
,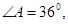 D在AB上,
D在AB上,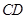 是
是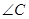 的平分线,则
的平分线,则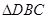 的面积与
的面积与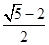
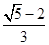
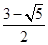
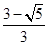
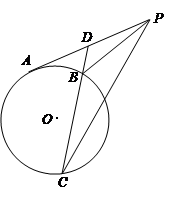
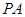 是圆
是圆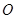 的切线,切点为
的切线,切点为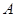 ,直线
,直线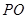 交圆
交圆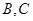 两点,
两点,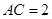 ,
,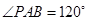 ,则圆
,则圆
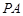 与⊙
与⊙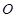 相切于点
相切于点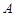 ,
,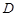 为
为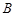 ,
,
 两点,若
两点,若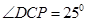 ,则
,则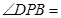 .
.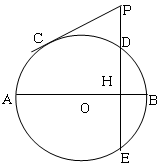
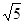 ,求PD的长.
,求PD的长.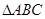 ,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则
,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则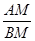 =( )
=( )