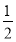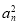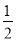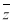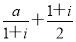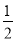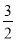题目内容
设f(x)＝x＋ax2＋bln x，曲线y＝f(x)过点
P(1,0)，且在P点处的切线的斜率为2.
①求a，b的值；
②证明：f(x)≤2x－2.
①a＝－1，b＝3.②见解析
【解析】① f′(x)＝1＋2ax＋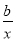
.
由题意知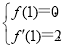
即
，
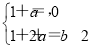解得a＝－1，b＝3.
②由①知f(x)＝x－x2＋3ln x.
f(x)的定义域为(0，＋∞)．
设g(x)＝f(x)－(2x－2)＝2－x－x2＋3ln x，
则g′(x)＝－1－2x＋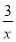
＝－
.?
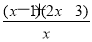由g′(x)>0知0<x<1，
由g′(x)<0知x>1.
所以g(x)在(0,1)内单调递增，在(1，＋∞)内单调递减．
所以g(x)在(0，＋∞)上的最大值为g(1)＝0，
所以g(x)≤0，即f(x)≤2x－2.
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
