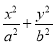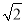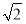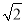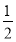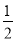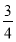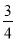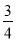题目内容
已知Sn为正项数列{an}的前n项和,且满足Sn=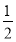
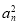 +
+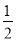 an(n∈
an(n∈
N+),求出a1,a2,a3,a4,猜想{an}的通项公式并给出证明
a1=1,a2=2,a3=3,a4=4,an=n.
【解析】由Sn=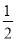
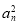 +
+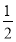 an(n∈N+).
an(n∈N+).
可得a1=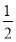
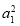 +
+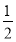 a1,解得a1=1,
a1,解得a1=1,
S2=a1+a2=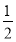
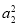 +
+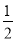 a2,解得a2=2,
a2,解得a2=2,
同理a3=3,a4=4,猜想an=n.
Sn=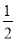
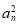 +
+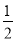 an①
an①
Sn-1=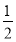
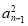 +
+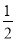 an-1,(当n≥2时)②
an-1,(当n≥2时)②
①-②得(an-an-1-1)(an+an-1)=0,
∵an+an-1≠0,∴an-an-1=1,
又a1=1,故数列{an}是首项a1=1,公差d=1的等差数列,
故an=n.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目